如图是无锡某比赛场馆的平面图,根据距离比赛场地的远近和视角的不同,将观赛场地划分成A、B、C三个不同的票价区.其中与场地边缘MN的视角大于或等于45°,并且距场地边缘MN的距离不超过15米的区域划分为A票区,B票区(如图1所示),剩下的为C票区.
(1)请你利用尺规作图,在观赛场地中,作出A票区所在的区域(只要求作出图形,保留作图痕迹,不要求写作法);
(2)如果每个座位所占的平均面积是1.2平方米,请估算A票区有多少个座位;
(3)为提高B区观众的观赛效果,举办方将B区用两个大型的支柱AP、AC撑起一定的角度,其横截面如图2所示.若AB=10米,∠B=30°,∠CPA=∠CAD=75°,求CP的长度.(结果保留根号)
先化简 ,再从-2<x<3中选一个合适的整数代入求值。
,再从-2<x<3中选一个合适的整数代入求值。
如图①,Rt△ABC中,∠B=900,∠CAB=300,它的顶点A的坐标为(10,0),顶点B的坐标为 (5,5 ) ,AB=10,点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
) ,AB=10,点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
(1)求∠BAO的度数.
(2)当点P在AB上运动时,△OPQ的面积S(平方单位)与时间t(秒)之间的函数图象为抛物线的一部分,(如图②),求点P的运动速度.
(3)求(2)中面积S与时间t之间的函数关系式及面积S取最大值时点P的坐标.
(4)如果点P,Q保持(2)中的速度不变,那么点P沿AB边运动时,∠OPQ的大小随着时间t的增大而增大;沿着BC边运动时,∠OPQ的大小随着时间t的增大而减小,当点P沿这两边运动时,使∠OPQ=90°的点P有几个?请说明理由.
我市某镇的一种特产由于运输原因,长期只能在当地销售.当地政府对该特产的销售投资收益为:每投入x万元,可获得利润P= (万元).当地政府拟在“十二•五”规划中加快开发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投入100万元的销售投资,在实施规划5年的前两年中,每年都从100万元中拨出50万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售.在外地销售的投资收益为:每投入x万元,可获利润Q=
(万元).当地政府拟在“十二•五”规划中加快开发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投入100万元的销售投资,在实施规划5年的前两年中,每年都从100万元中拨出50万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售.在外地销售的投资收益为:每投入x万元,可获利润Q= (万元)
(万元)
(1)若不进行开发,求5年所获利润的最大值是多少?
(2)若按规划实施,求5年所获利润(扣除修路后)的最大值是多少?
(3)根据(1)(2),该方案是否具有实施价值?
已知关于x的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a,b,c分别为△ABC三边的长.
(1)如果x=-1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
如图,抛物线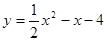 与坐标轴相交于
与坐标轴相交于 、
、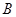 、
、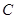 三点,
三点,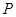 是线段
是线段 上一动点(端点除外),过
上一动点(端点除外),过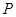 作
作 ,交
,交 于点
于点 ,连接
,连接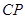 .
.
(1)直接写出 、
、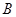 、
、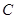 的坐标;
的坐标;
(2)求抛物线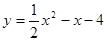 的对称轴和顶点坐标;
的对称轴和顶点坐标;
(3)求 面积的最大值,并判断当
面积的最大值,并判断当 的面积取最大值时,以
的面积取最大值时,以 、
、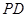 为邻边的平行四边形是否为菱形.
为邻边的平行四边形是否为菱形.