如图1所示，A和B是真空中两块面积很大的平行金属板、加上交变电压，在两板间产生变化的电场。已知B板电势为零，在0～T时间内，A板电势UA随时间变化的规律如图2所示，其中UA的最大值为U0，最小值为 -2U0 。在图1中，虚线MN表示与A、B板平行且等距的一个较小的面，此面到A和B的距离皆为L。在此面所在处，不断地产生电量为q、质量为m的带负电微粒，微粒随时间均匀产生出来。微粒产生后，从静止出发在电场力的作用下运动。设微粒一旦碰到金属板，就附在板上不再运动，且其电量同时消失，不影响A、B板的电压。已知在0～T时间内产生出来的微粒，最终有四分之一到达了A板，求这种微粒的比荷（q/m）。（不计微粒重力，不考虑微粒之间的相互作用）。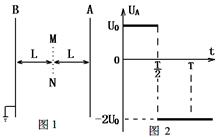
将一个小球以
的速度沿水平方向抛出，小球经过
的时间落地。不计空气阻力作用。求：
（1）抛出点与落地点在竖直方向的高度差；
（2）小球落地时的速度大小
（3）以地面为零势能面，离地多高时动能是势能的3倍。
一列简谐横波在x轴上传播，在t1＝0和t2＝0.5 s两时刻的波形分别如图中的实线和虚线所示，求：
(1)周期
(2)波速
(3)若波速为92 m/s，求波的传播方向．
发电机输出功率为100 kW，输出电压是250 V，用户需要的电压是220 V，输电线电阻为10 Ω.若输电线中因发热而损失的功率为输送功率的4%，试求：
(1)用户得到的电功率是多少
(2)在输电线路中设置的升、降压变压器原副线圈的匝数比
有n=10匝的矩形线圈，每匝都是长50cm，宽20cm，线圈总电阻10Ω，在B=2T的匀强磁场中以角速度ω=50rad／s旋转.线圈与R=40Ω的外电阻连接，图中的电流表、电压表的接入不影响原电路.求：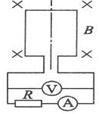
(1)流过电阻电流的瞬时表达式(从中性面开始计时)
(2)电流表、电压表的读数
(3)电路中1min内产生的热量
(4)从图示位置开始计时转过90度的过程中流过安培表的电量。
某发电厂输出功率为100 kW，输电线电阻为4Ω，求当以2000伏和2万伏输送时电路分别损失的电功率为多少?