如图，AB=AC，AD=AE，BD、CE交于O，求证AO平分∠BAC.
△ABC的外角∠CBD，∠BCE的角平分线交于点F，求证AF平分∠BAC.
如图，P为∠AOB内一点，OA=OB，且△OPA与△OPB面积相等，求证∠AOP=∠BOP.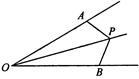
古代有一位商人有一块三角形土地，土地的一边靠水渠，如图所示，现在他想把这块土地平均分给他的三个儿子，为使土地灌溉方便，想使每个儿子分得的土地都有一边和水渠相邻.试问应如何分割这块土地？请你说明理由。
如图，在△ABC中，若AD是BC边上的中线，则有BD ==
，若过A点作BC边上的高AE，利用三角形的面积公式可求得S△ABD==S△ABC，请你任意画一个三角形，将这个三角形的面积四等分。
其中
不等式组
的整数解.