我县某包装生产企业承接了一批上海世博会的礼品盒制作业务,为了确保质量,该企业进行试生产。他们购得规格是170cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材。如图所示,(单位:cm)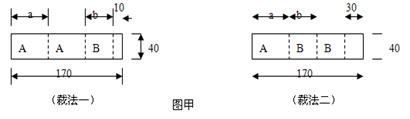
(1)列出方程(组),求出图甲中a与b的值。
(2)在试生产阶段,若将30张标准板材用裁法一裁剪,4张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成图乙的竖式与横式两种无盖礼品盒。
①两种裁法共产生A型板材 张,B型板材 张;
②设做成的竖式无盖礼品盒x个,横式无盖礼品盒的y个,根据题意完成表格:
| 礼品盒 板 材 |
竖式无盖(个) |
横式无盖(个) |
| x |
y |
|
| A型(张) |
4x |
3y |
| B型(张) |
x |
|
③做成的竖式和横式两种无盖礼品盒总数最多是 个;此时,横式无盖礼品盒可以做 个。(在横线上直接写出答案,无需书写过程)
如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E.
(1)求证:CE是⊙O的切线;
(2)若AE=1,CE=2,求⊙O的半径.

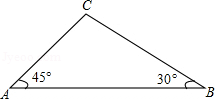
如图,天星山山脚下西端A处与东端B处相距 米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为 米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
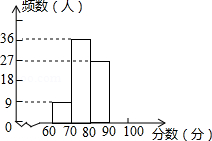
秋季新学期开学时,红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了如下不完整的图表:
|
分 数 段 |
频数 |
频率 |
|
60≤x<70 |
9 |
a |
|
70≤x<80 |
36 |
0.4 |
|
80≤x<90 |
27 |
b |
|
90≤x≤100 |
c |
0.2 |
请根据上述统计图表,解答下列问题:
(1)在表中,a= ,b= ,c= ;
(2)补全频数直方图;
(3)根据以上选取的数据,计算七年级学生的平均成绩.
(4)如果测试成绩不低于80分者为“优秀”等次,请你估计全校七年级的800名学生中,“优秀”等次的学生约有多少人?
如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.

(1)计算: .
(2)解不等式组 .