若不等式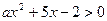 的解集是
的解集是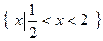 ,求不等式
,求不等式 的解集。
的解集。
已知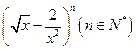 的展开式中,第5项的系数与第3项的系数比是10:1
的展开式中,第5项的系数与第3项的系数比是10:1
求:(1 ) 展开式中含
) 展开式中含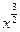 的项
的项
(2) 展开式中二项式系数最大的项
(3) 展开式中系数最大的项
一个袋中有10个大小相同的黑球、白球和红球,已知从袋中任意摸出一个球,得到黑球的概率是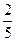 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是
(1)求袋中白球的个数;
(2)若将其中的红球拿出,从剩余的球中一次摸出3个球,求恰好摸到2个白球的概率;
(3)在(2)的条件下,一次摸出3个球,求取得白球数X的数学期望。
设 ,
,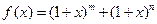 ,
,
(1)当
 时,若
时,若
求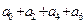 。
。
(2)当 时,若
时,若 展开
展开 式中
式中 的系数是20,求
的系数是20,求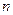 的值。
的值。
(3) 展开式中
展开式中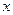 的系数是19,当
的系数是19,当 ,
,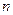 变化时,求
变化时,求 系数的最小值。
系数的最小值。
已知男人中有5%患色盲,女人中有0.25%患色盲,从100个男人和100个女人中任选一人.
(1)求此人患色盲的概率;
(2)如果此人是色盲,求此人是男人的概率.(以上各问结果写成最简分式形式)