如图所示,质量为4kg的小球用细绳拴着吊在行驶的汽车后壁上,绳与竖直方向夹角为37º。已知g = 10m/s2,sin37º=0.6,cos37º=0.8,求:
(1)汽车匀速运动时,细线对小球的拉力和车后壁对小球的压力。
(2)当汽车以a=2m/s2向右匀减速行驶时,细线对小球的拉力和小球对车后壁的压力。
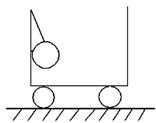
如图所示,水平传送带以一定速度匀速运动,将质量m=1kg的小物块轻轻放在传送带上的P点,物块运动到A点后被水平抛出,小物块恰好无碰撞地沿圆弧切线从B点进入竖直光滑圆弧轨道下滑.B、C为圆弧上的两点,其连线水平,已知圆弧对应圆心角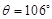 ,A点距水平面的高度h=0.8m.小物块到达C点时的速度大小与B点相等,并沿固定斜面向上滑动,小物块从C点到第二次经过D点的时间间隔为0.8s,已知小物块与斜面间的动摩擦因数
,A点距水平面的高度h=0.8m.小物块到达C点时的速度大小与B点相等,并沿固定斜面向上滑动,小物块从C点到第二次经过D点的时间间隔为0.8s,已知小物块与斜面间的动摩擦因数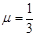 ,重力加速度g取10 m/s2,取
,重力加速度g取10 m/s2,取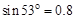 ,cos53°=0.6,求:
,cos53°=0.6,求: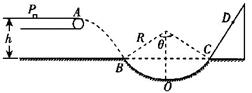
(1)小物块从A到B的运动时间;
(2)小物块离开A点时的水平速度大小;
(3)斜面上C、D点间的距离.
如图甲所示为一风力实验示意图.开始时,质量为m="1" kg的小球穿在固定的足够长的水平细杆上,并静止于O点.现用沿杆向右的恒定风力F作用于小球上,经时间t1="0.4" s后撤去风力.小球沿细杆运动的v-t图象如图乙所示(g取10 m/s2) .试求:

(1)小球沿细杆滑行的距离;
(2)小球与细杆之间的动摩擦因数;
(3)风力F的大小.
(10分)如图所示,A、B两球完全相同,质量均为m,用两根等长的细线悬挂在O点,两球之间固连着一根劲度系数为k的轻弹簧,两球静止时,弹簧位于水平方向且与AB两球心连线共线,两根细线之间的夹角为 ,求:
,求: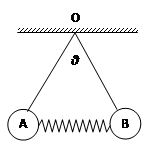
(1)细线中拉力的大小;
(2)弹簧长度的压缩量.
(16分)如图所示,空间存在一个方向垂直桌面向下的磁场。现将质量为 、边长为
、边长为 的正方形线框
的正方形线框 ,静止放在光滑绝缘足够大的水平桌面上,
,静止放在光滑绝缘足够大的水平桌面上, 边与
边与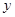 轴重合。
轴重合。 边的电阻为
边的电阻为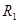 ,
, 边的电阻为
边的电阻为 ,线框其余部分电阻不计。
,线框其余部分电阻不计。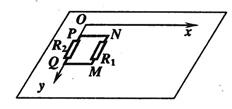
(1)若磁场随时间的变化规律为 (
( 为大于零的已知常数),求线框中感应电流的大小和方向。
为大于零的已知常数),求线框中感应电流的大小和方向。
(2)若磁场不随时间变化,而是按照下列情况分布:磁感应强度沿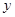 轴方向均匀分布,沿
轴方向均匀分布,沿 轴方向按规律
轴方向按规律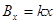 变化(
变化( 为大于零的已知常数),线框从
为大于零的已知常数),线框从 =0时刻、以初速度
=0时刻、以初速度 由图示位置向
由图示位置向 轴正方向平动。求在图示位置线框所受安培力的大小和方向。
轴正方向平动。求在图示位置线框所受安培力的大小和方向。
(3)在第(2)问中,若 ,求在整个运动过程中,电阻
,求在整个运动过程中,电阻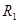 产生的焦耳热。
产生的焦耳热。
(16分)如图甲所示,在 轴右侧加有垂直纸面向外的匀强磁场,磁感应强度
轴右侧加有垂直纸面向外的匀强磁场,磁感应强度 =1T。从原点
=1T。从原点 处向第Ⅰ象限发射一比荷
处向第Ⅰ象限发射一比荷 =1×104C/kg的带正电的粒子(重力不计),速度大小
=1×104C/kg的带正电的粒子(重力不计),速度大小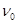 =103m/s,方向垂直于磁场且与
=103m/s,方向垂直于磁场且与 轴正方向成300角。
轴正方向成300角。

(1)求粒子在该匀强磁场中做匀速圆周运动的半径 和在该磁场中运动的时间
和在该磁场中运动的时间 。
。
(2)若磁场随时间变化的规律如图乙所示(垂直于纸面向外为正方向), s后空间不存在磁场.在
s后空间不存在磁场.在 =0时刻,粒子仍从
=0时刻,粒子仍从 点以与原来相同的速度
点以与原来相同的速度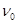 射入,求粒子从
射入,求粒子从 点射出后第2次经过
点射出后第2次经过 轴时的坐标。
轴时的坐标。