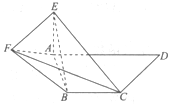
已知数列{an}的前n项和为Sn,且Sn= ,n∈N﹡,数列{bn}满足an=4log2bn+3,n∈N﹡。
,n∈N﹡,数列{bn}满足an=4log2bn+3,n∈N﹡。
(1)求an,bn;
(2)求数列{an·bn}的前n项和Tn。
(本小题满分12分)
已知函数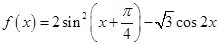 ,
,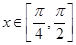 .设
.设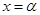 时
时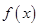 取到最大值.
取到最大值.
(1)求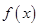 的最大值及
的最大值及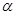 的值;
的值;
(2)在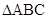 中,角
中,角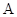 ,
,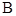 ,
, 所对的边分别为
所对的边分别为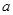 ,
, ,
, ,
, ,且
,且 ,求
,求 的值.
的值.
(本小题满分10分)
已知函数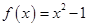 ,
,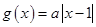 .
.
(1)若关于 的方程
的方程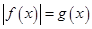 只有一个实数解,求实数
只有一个实数解,求实数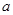 的取值范围;
的取值范围;
(2)若当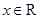 时,不等式
时,不等式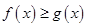 恒成立,求实数
恒成立,求实数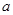 的取值范围.
的取值范围.
(本小题满分10分)
如图,已知圆 是
是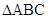 的外接圆,
的外接圆,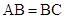 ,
,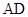 是
是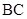 边上的高,
边上的高,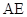 是圆
是圆 的直径.过点
的直径.过点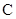 作圆
作圆 的切线交
的切线交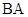 的延长线于点
的延长线于点 .
.
(1)求证: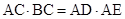 ;
;
(2)若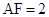 ,
,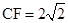 ,求
,求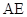 的长.
的长.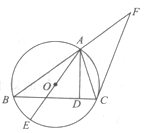
(本小题满分12分)
已知函数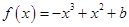 ,
,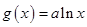 .
.
(1)若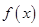 在
在 上的最大值为
上的最大值为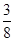 ,求实数
,求实数 的值;
的值;
(2)若对任意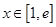 ,都有
,都有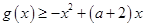 恒成立,求实数
恒成立,求实数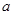 的取值范围;
的取值范围;
(3)在(1)的条件下,设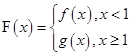 ,对任意给定的正实数
,对任意给定的正实数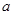 ,曲线
,曲线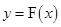 上是否存在两点
上是否存在两点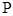 、
、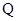 ,使得
,使得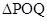 是以
是以 (
( 为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在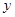 轴上?请说明理由.
轴上?请说明理由.
(本题小满分12分)
如图,在直角梯形 中,
中,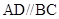 ,
, ,
, 平面
平面 ,
,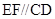 ,
,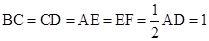 .
.
(1)求证: 平面
平面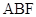 ;
;
(2)在直线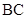 上是否存在点
上是否存在点 ,使二面角
,使二面角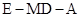 的大小为
的大小为 ?若存在,求出
?若存在,求出 的长;若不存在,说明理由.
的长;若不存在,说明理由.