已知:如图10,AB和DE是直立在地面上的两根立柱,AB="5" m,某一时刻,AB在阳光下的投影BC="4" m.
(1)请你在图中画出此时DE在阳光下的投影,并简述画图步骤;
(2)在测量AB的投影长时,同时测出DE在阳光下的投影长为6 m,请你计算DE的长.
有这样一个问题:探究函数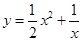 的图象与性质.
的图象与性质.
小东根据学习函数的经验,对函数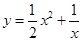 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数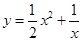 的自变量x的取值范围是____;
的自变量x的取值范围是____;
(2)下表是y与x的几组对应值.
求m的值:
(3)如下图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象:
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是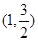 ,结合函数的图象,写出该函数的其它性质(一条即可):_________.
,结合函数的图象,写出该函数的其它性质(一条即可):_________.
阅读下列材料:
2015年清明小长假,北京市属公园开展以“清明踏青,春色满园”为主题的游园活动,虽然气温小幅走低,但游客踏青赏花的热情很高,市属公园游客接待量约为190万人次,其中,玉渊潭公园的樱花、北京植物园的桃花受到了游客的热捧,两公园的游客接待量分别为28万人次、21.75万人次;颐和园、天坛公园、公园因皇家园林的厚重文化底蕴与满园春色成为游客的重要目的地,游客接待量分别为26万人次、20万人次、17.6万人次;北京动物园游客接待量为18万人次,熊猫馆的游客密集度较高.
2014年清明小长假,天气晴好,北京市属公园游客接待量约为200万人次,其中,玉渊潭公园游客接待量比2013年清明小长假增长了25%;颐和园游客接待量为26.2万人次,比2013年清明小长假增加了4.6万人次;北京动物园游客接待量为22万人次.
2013年清明小长假,玉渊潭公园、陶然亭公园、北京动物园游客接待量分别为32万人次,13万人次、14.9万人次.
根据以上材料解答下列问题:
(1)2014年清明小长假,玉渊潭公园游客接待量为____万人次;
(2)选择统计表或统计图,将2013-2015年清明小长假玉渊潭公园、颐和园和北京动物园的游客接待量表示出来.
如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD//BM,交AB于点F,且 ,连接AC,AD,延长AD交BM于点E.
,连接AC,AD,延长AD交BM于点E.
(l)求证:△ACD是等边三角形;
(2)连接OE,若DE=2,求OE的长.
在□ABCD,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
为解决“最后一公里”的交通接驳问题,北京市投放了大量公租自行车供市民使用.到2013年底,全市已有公租自行车25000辆,租赁点600个.预计到2015年底,全市将有公租自行车50000辆,并且平均每个租赁点的公租自行车数量是2013年成平均每个租赁点的公租自行车数量的1.2倍.预计2015年底,全市将租赁点多少个?