已知变量y与2x成反比例，且当x=2时，y=6，
（1）求y与x之间的函数关系．
（2）请判断点B（3，4）是否在这个反比例函数的图象上，并说明理由．
如图，已知△ABC内接于⊙O，∠BAC=60°，AD⊥BC于D，BE⊥AC于E交AD于H，若CF是⊙O的直径，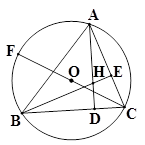
（1）求∠FCB的度数；
（2）求证：AH=
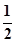CF.
已知二次函数y=ax2+bx+c（a≠0）的图象过点A（2,0），B（－2，－4），对称轴为直线x=－1. （1）求这个二次函数的解析式；
（2）若-3<x<3，直接写出y的取值范围；
（3）若一元二次方程ax2+bx+c－m=0（a≠0，m为实数）在-3<x<3的范围内有实数根，直接写出m的取值范围.
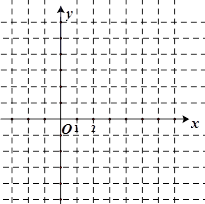
对于抛物线y=x2－4x+3，（1）与y轴的交点坐标是___________,与x轴的交点坐标是_______________,
顶点坐标是____________.（2）在坐标系中利用描点法画出此抛物线.
| x |
... |
... |
|||||
| y |
... |
... |
已知二次函数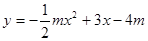
的图象与x轴交于点A（4,0）、点B，与y轴交于
点C。（1）求此二次函数的解析式及点B的坐标；
（2）点P从点A出发以每秒1个单位的速度沿线段AO向O点运动，到达点O后停止运动，过点P作PQ//AC交OC于点Q，将四边形PQCA沿PQ翻折，得到四边形
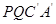,设点P的运动时间为t。
①当t为何值时，点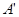
恰好落在二次函数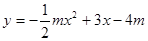的图象的对称轴上；
②设四边形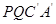落在第一象限内的图形面积为S，求S关于t的函数关系式，并求出当t为何值时S的值最大。
如图：点O是等边△ABC内一点，∠AOB=110°，∠BOC=α.将线段OC绕点[来C按顺时针方向旋转60°得到线段CD，连接OD、AD.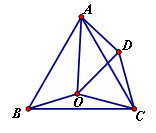
(1)求证：AD=BO
（2）当α=150°时，试判断△AOD的形状，并说明理由；
（3）探究：当α为多少度时（直接写出答案），△AOD是等腰三角形？