利用图形来表示数量或数量关系,也可以利用数量或数量关系来描述图形特征或图形之间的关系,这种思想方法称为数形结合.我们刚学过的《从面积到乘法公式》就很好地体现了这一思想方法,你能利用数形结合的思想解决下列问题吗?
如图,一个边长为1的正方形,依次取正方形的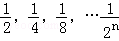 ,根据图示我们可以知道:第一次取走
,根据图示我们可以知道:第一次取走 后还剩
后还剩 ,即
,即 =1﹣
=1﹣ ;前两次取走
;前两次取走 +
+ 后还剩
后还剩 ,即
,即 +
+ =1﹣
=1﹣ ;前三次取走
;前三次取走 +
+ +
+ 后还剩
后还剩 ,即
,即 +
+ +
+ =1﹣
=1﹣ ;…前n次取走后,还剩 _________ ,即 _________ = _________ .
;…前n次取走后,还剩 _________ ,即 _________ = _________ .
利用上述计算:
(1) = _________ .
= _________ .
(2) = _________ .
= _________ .
(3)2﹣22﹣23﹣24﹣25﹣26﹣…﹣22011+22012(本题写出解题过程)
一个不透明的布袋中装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同。
(1) 摸一个球,记下颜色后放回,并拌匀,在摸出一个球,求两次摸出的球颜色恰好不同的概率(要求用树状图或列表法说明)。
(2) 再将n个白球放入袋中,拌匀,使摸出一个球是白球的概率是 ,求n的值。
,求n的值。
聪明的你试试看吧!
(1)分析图①,②,④中阴影部分的分布规律,按此规律在图③中画出其中的阴影部分。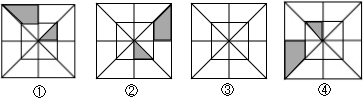
(2)在下列的图形上补一个小正方形,使它成为一个轴对称图形。
如图, △ABC中AD是BC边上的高,CE是△ABC的一条角平分线, 它们相交于点P. 已知∠APE=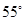 , ∠AEP=
, ∠AEP=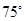 , 求△ABC的各个内角的度数。
, 求△ABC的各个内角的度数。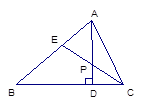
细心算一算。(每小题5分,共10分)
(1)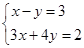 (2)
(2)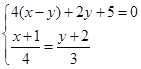
如图,P是∠BAC的平分线上的一点,PB⊥AB,PC⊥AC,试说明PB=PC的理由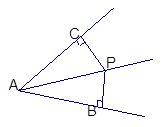
解:在△APB和△APC中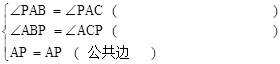
∴△APB≌△APC ( )
∴PB=PC()