九(1)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
月均用水量 (t) (t) |
频数(户) |
频率 |
 |
6 |
0.12 |
 |
|
0.24 |
 |
16 |
0.32 |
 |
10 |
0.20 |
 |
4 |
|
 |
2 |
0.04 |

请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)求该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计该小区月均用水量超过20t的家庭大约有多少户?
某校为了解七年级学生的体重情况,随机抽取了七年级 名学生进行调查,将抽取学生的体重情况绘制如下不完整的频数分布表和扇形统计图.
|
组别 |
体重(千克) |
人数 |
|
|
|
10 |
|
|
|
|
|
|
|
40 |
|
|
|
20 |
|
|
|
10 |
请根据图表信息回答下列问题:
(1)填空:
① ,
② ,
③在扇形统计图中, 组所在扇形的圆心角的度数等于 度;
(2)若把每组中各个体重值用这组数据的中间值代替(例如: 组数据中间值为40千克),则被调查学生的平均体重是多少千克?
(3)如果该校七年级有1000名学生,请估算七年级体重低于47.5千克的学生大约有多少人?
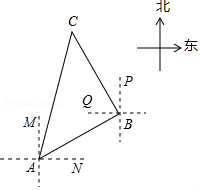
如图,一艘船由 港沿北偏东 方向航行 至 港,然后再沿北偏西 方向航行 至 港.
(1)求 , 两港之间的距离(结果保留到 ,参考数据: , ;
(2)确定 港在 港的什么方向.
某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同,求该工厂原来平均每天生产多少台机器?
已知直线 分别交 轴、 轴于 、 两点,抛物线 经过点 ,和 轴的另一个交点为 .

(1)求抛物线的解析式;
(2)如图1,点 是抛物线上的动点,且在第三象限,求 面积的最大值;
(3)如图2,经过点 的直线交抛物线于点 、 ,连接 、 分别交 轴于点 、 ,求 的值.
备注:抛物线顶点坐标公式 ,
如图,在矩形 中, , ,点 是 边上的点, ,连接 , 交于点 .
(1)求证: ;
(2)连接 ,求 的值;
(3)连接 交 于点 ,求 的值.
