如图，在Rt△ABC中，∠A＝90º，AB＝6cm，AC＝8cm，D、E分别是边AB、AC的中点，点P从点D出发沿DE方向以1cm/s的速度运动，过点P作PQ⊥BC于Q，过点Q作QR∥BA交AC于R、交DE于G，当点Q与点C重合时，点P停止运动．设点P运动时间为ts．
（1）点D到BC的距离DH的长是 ；
（2）当四边形BQGD是菱形时，t= ，S△EGR= ；
（3）令QR＝y，求y关于t的函数关系式（不要求写出自变量的取值范围）；
（4）是否存在点P，使△PQR为等腰三角形？若存在，请求出所有满足要求的t的值；若不存在，请说明理由．
袋中装有大小相同的2个红球和2个绿球，
（1）先从袋中摸出1个球后放回，混合均匀后再摸出1个球，
① 求第一次摸到绿球，第二次摸到红球的概率；
② 求两次摸到的球中有1个绿球和1个红球的概率；
（2）先从袋中摸出1个球后不放回，再摸出1个球，则两次摸到的球中有1个绿球和1个红球的概率是多少？请直接写出结果.
如图，在直角坐标系中，A(0，4)、C(3，0)，
（1）① 画出线段AC关于y轴对称线段AB；
② 将线段CA绕点C顺时针旋转一个角，得到对应线段CD，使得AD∥x轴，请画出线段CD；
（2）若直线y＝kx平分(1)中四边形ABCD的面积，请直接写出实数k的值.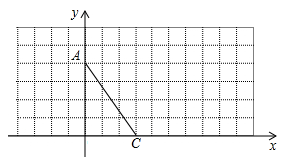
如图，
和
相交于点
，
，
，求证：
.
已知直线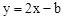
经过点(1，－1)，求关于x的不等式2x－b≥0的解集.
解方程：
.