如图所示是一种测量通电线圈中磁场的磁感应强度B的装置,把一个很小的测量线圈A放在待测处,线圈与测量电荷量的冲击电流计G串联,当用双刀双掷开关S使螺线管的电流反向时,测量线圈中就产生感应电动势,从而引起电荷的迁移,由表G测出电荷量Q,就可以算出线圈所在处的磁感应强度B.已知测量线圈的匝数为N,直径为d,它和表G串联电路的总电阻为R,则被测出的磁感应强度B为多大?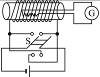
如图,体积为V、内壁光滑的圆柱形导热气缸顶部有一质量和厚度均可忽略的活塞;气缸内密封有温度为2.4T0、压强为1.2p0的理想气体.p0和T0分别为大气的压强和温度.已知:气体内能U与温度T的关系为U=αT,α为正的常量;容器内气体的所有变化过程都是缓慢的.求:
①气缸内气体与大气达到平衡时的体积V1;
②在活塞下降过程中,气缸内气体放出的热量Q.
许多仪器中可利用磁场控制带电粒子的运动轨迹.在如图所示的真空环境中,有一半径r=0.05m的圆形区域内存在磁感应强度B=0.2T的匀强磁场,其右侧相距d=0.05m处有一足够大的竖直屏.从S处不断有比荷 =1×108C/kg的带正电粒子以速度v=2×106m/s沿SQ方向射出,经过磁场区域后打在屏上.不计粒子重力.求:
=1×108C/kg的带正电粒子以速度v=2×106m/s沿SQ方向射出,经过磁场区域后打在屏上.不计粒子重力.求:
(1)粒子在磁场中做圆周运动的轨迹半径;
(2)绕通过P点(P点为SQ与磁场边界圆的交点)垂直纸面的轴,将该圆形磁场区域逆时针缓慢移动90°的过程中,粒子在屏上能打到的范围.
如图所示,一个水平放置的圆桶正以中心轴匀速运动,桶上有一小孔,桶壁很薄,当小孔运动到桶的上方时,在孔的正上方h处有一个小球由静止开始下落,已知圆孔的半径略大于小球的半径,为了让小球下落时不受任何阻碍,h与桶的半径R之间应满足什么关系(不考虑空气阻力)?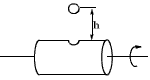
如图甲所示, 、
、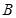 为水平放置的间距
为水平放置的间距 的两块足够大的平行金属板,两板间有场强为
的两块足够大的平行金属板,两板间有场强为 、方向由
、方向由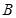 指向
指向 的匀强电场.一喷枪从
的匀强电场.一喷枪从 、
、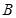 板的中央点
板的中央点 向水平线各个方向均匀地喷出初速度大小均为
向水平线各个方向均匀地喷出初速度大小均为 的带电微粒.已知微粒的质量均为
的带电微粒.已知微粒的质量均为 、电荷量均为
、电荷量均为 ,不计微粒间的相互作用、对板间电场和磁场的影响及空气阻力,取
,不计微粒间的相互作用、对板间电场和磁场的影响及空气阻力,取 .求:
.求: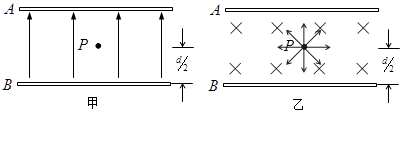
(1)微粒落在金属板上所围成的图形面积.
(2)要使微粒不落在金属板上,通过计算说明如何调节两板间的场强.
(3)在满足(2)的情况下,在两板间加垂直于纸面向里的匀强磁场,磁感应强度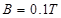 ,调节喷枪使微粒可以向纸面内沿各个方向喷出(如图乙),求
,调节喷枪使微粒可以向纸面内沿各个方向喷出(如图乙),求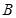 板被微粒打中的区域长度和微粒在磁场中运动的最短时间.
板被微粒打中的区域长度和微粒在磁场中运动的最短时间.
如图示,滑板A放在水平面上,长度为 ,滑块质量mA=1 kg、mB=0.99 kg,A、B间粗糙,现有mC="0.01" kg子弹以V0=200m/s速度向右击中B并留在其中,求
,滑块质量mA=1 kg、mB=0.99 kg,A、B间粗糙,现有mC="0.01" kg子弹以V0=200m/s速度向右击中B并留在其中,求
(1)子弹C击中B后瞬间,B速度多大
(2)若滑块A与水平面固定,B被子弹击中后恰好滑到A右端静止,求滑块B与A间动摩擦因数μ
(3)若滑块A与水平面光滑,B与A间动摩擦因数不变,试分析B能否离开啊, 并求整个过程A、B、C组成的系统损失的机械能