如图所示,用两根长度都为l的细线悬挂一个小球A,两悬挂点等高,线与水平天花板间的夹角都是α,使球A在垂直于纸面的平面内做小幅度的摆动,当A经过平衡位置的瞬间,另一小球B从A球的正上方自由下落,若B球恰能击中A球,求B球开始下落时离A球振动平衡位置的高度。
如图所示,电源的电动势E=24 V,内阻r=1 Ω,电阻R=2 Ω,M为直流电动机,其电阻r′=1 Ω,电动机正常工作时,其两端所接电压表读数为UV=21 V,求电动机所做机械功的功率是多少?
如图所示,四分之一光滑绝缘圆弧轨道AP和水平绝缘传送带PC固定在同一竖直平面内,圆弧轨道的圆心为O,半径为R。静止的传送带PC之间的距离为L,在OP的左侧空间存在方向竖直向下的匀强电场,场强大小为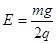 。一质量为m、电荷量为+q的小物体从圆弧顶点A由静止开始沿轨道下滑,恰好运动到C端后返回。不计物体经过轨道与传送带连接处P时的机械能损失,重力加速度为g。求:
。一质量为m、电荷量为+q的小物体从圆弧顶点A由静止开始沿轨道下滑,恰好运动到C端后返回。不计物体经过轨道与传送带连接处P时的机械能损失,重力加速度为g。求: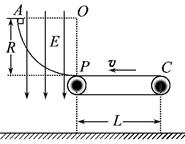
(1)物体运动到P点的速度大小;
(2)物体与传送带间的动摩擦因数μ;
(3)若传送带沿逆时针方向传动,传送带速度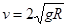 ,则物体第一次返回到圆弧轨道P点时物体对圆弧轨道的压力大小;
,则物体第一次返回到圆弧轨道P点时物体对圆弧轨道的压力大小;
如图所示,两带电平行金属板A、B与竖直方向成30°角放置,两板间电势差 =500V。B板中心有一小孔正好位于平面直角坐标系 xOy上的O点,y轴沿竖直方向。一比荷为1.0×105C/kg的带正电粒子P,从A板中心
=500V。B板中心有一小孔正好位于平面直角坐标系 xOy上的O点,y轴沿竖直方向。一比荷为1.0×105C/kg的带正电粒子P,从A板中心 处静止释放后沿垂直于金属板的直线
处静止释放后沿垂直于金属板的直线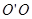 进入x轴下方第四象限的匀强电场E中,场强方向与AB板平行且斜向上。粒子穿过电场后,从坐标P(1m,0)处离开电场,粒子的重力不计(如有需要:
进入x轴下方第四象限的匀强电场E中,场强方向与AB板平行且斜向上。粒子穿过电场后,从坐标P(1m,0)处离开电场,粒子的重力不计(如有需要: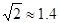 、
、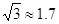 、
、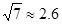 )。试求:
)。试求: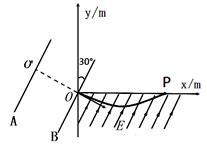
(1)粒子刚进入匀强电场时的速度大小;
(2)匀强电场的场强E的大小;
(3)求粒子离开电场时的速度大小;
如图所示的电路中,电源电动势E = 6.0V,内阻r = 1.0 ,电阻R2= 2.0
,电阻R2= 2.0 ,当开关S断开时,电流表的示数为1.0A ,电压表的示数为2.0V ,试求:
,当开关S断开时,电流表的示数为1.0A ,电压表的示数为2.0V ,试求:
(1)电阻R3的阻值;
(2)电阻R1消耗的功率;
(3)当开关S闭合后,经过10s,电阻R2产生的热量;
如图所示,在匀强电场中,将一电荷量为 C的正电荷由A点移到B点,其电势能减少了0.2J,已知A、B两点间距离为1m,两点连线与电场方向成600角,求:
C的正电荷由A点移到B点,其电势能减少了0.2J,已知A、B两点间距离为1m,两点连线与电场方向成600角,求:
(1)电荷由A移到B的过程中,电场力所做的功WAB;
(2)A、B两点间的电势差UAB;
(3)该匀强电场的电场强度E;