在“探究小车速度随时间变化的规律”的实验中，小车做匀加速直线运动，打点计时器接在50HZ的低压交变电源上。某同学在打出的纸带上每5点取一个计数点，共取了A、B、C、D、E、F六个计数点（每相邻两个计数点间的四个点未画出）。从每一个计数点处将纸带剪开分成五段（分别为a、b、c、d、e段），将这五段纸带由短到长紧靠但不重叠地粘在xoy坐标系中，如图所示，由此可以得到一条表示v-t关系的图线，从而求出加速度的大小。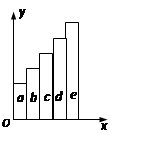
（1）请你在xoy坐标系中用最简洁的方法作出能表示v-t关系的图线（作答在答题纸的图上）；
（2）从第一个计数点开始计时，为求出0.15s时刻的瞬时速度，需要测出哪一段纸带的长度？答： _ ；
（3）若测得a段纸带的长度为2.0cm，e段纸带的长度为10.0cm，则可求出加速度的大小为 _ m/s2。
一物体在相互垂直的两个共点力Fl、F2作用下运动，运动过程中F1对物体做功3 J，F2对物体做功4 J，则F1与F2的合力对物体做功()
| A．l J | B．5 J | C．7 J | D．无法计算 |
用水平恒力F作用于质量为M的物体，使之在光滑的水平面上沿力的方向移动距离s，恒力做功为W1，再用此恒力作用于质量为m的物体上，使之在粗糙的水平面上移动同样距离s，恒力做功为W2，则两次此恒力做功的关系是()
| A．W1＞W2 | B．W1＜W2 | C．W1＝W2 | D．无法确定 |
如图所示，是小孩滑滑梯的情景，在小孩下滑过程中，关于各力做功的说法，不正确的是()
A．重力做正功
B．摩擦力做负功
C．支持力不做功
一列沿x轴传播的简谐机械波，其波源位于坐标原点O，振动方程为y=5sin4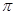
t(cm)，波长
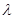="1O" m。则该波从坐标原点O点传播到x="5" m处所需的时间为
| A．0.25 s | B．O.5 s | C．1 s | D．2 s |
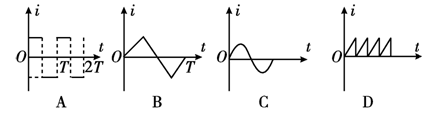
如图中不属于交变电流的是( )