已知数列{an}的各项均为正数，前n项的和Sn＝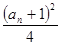
⑴ 求{an}的通项公式；
⑵ 设等比数列{bn}的首项为b，公比为2，前n项的和为Tn.若对任意n∈N*，Sn≤Tn
均成立，求实数b的取值范围．
已知函数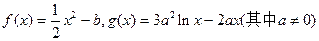
（I）求函数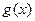
的单调递增区间；
（II）若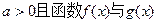
的图像有公共点，且在该点处的切线相同，用a表示b，并求b的最大值。
已知函数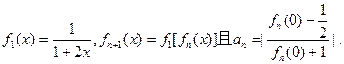
（I）求数列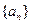
的通项公式；
（II）若数列
某学校有男教师150名，女教师100人，按照分层抽样的方法抽出5人进行一项问卷调查。
（I）求某老师被抽到的概率及5人中的男、女教师的人数；
（II）若从这5人中选出两人进行某项支教活动，则抽出的两人中恰有一名女教师的概率。
如图，DC⊥平面ABC，EB//DC，AC=BC=EB=2DC=2，∠ACB=120°，P，Q分别为AE、AB的中点。
（I）证明：PQ//平面ACD；
（II）求异面直线AE与BC所成角的余弦值；
（III）求AD与平面ABE所成角的正弦值；
若向量
，在函数
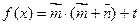的图象中，对称中心到对称轴的最小距离为
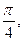且当
的最大值为1。
（I）求函数
的解析式；
（II）求函数的单调递增区间。