一竖直固定光滑的半圆形轨道ACB,圆心为O,半径为R。在最高点A把小球以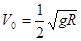 平抛,小球碰到轨道后不反弹(沿轨道径向速度减为0),忽略一切阻力,求:
平抛,小球碰到轨道后不反弹(沿轨道径向速度减为0),忽略一切阻力,求: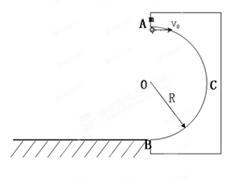
①.小球打到轨道上D点(图中未画出)时下落的高度;
②.小球到达最低点B时速度和对轨道的压力。
如图所示,匀强电场区域和匀强磁场区域是紧邻的且宽度相等均为d,电场方向在纸平面内竖直向下,而磁场方向垂直纸面向里,一带正电粒子从O点以速度v0垂直电场方向进入电场,从A点出电场进入磁场离开电场时带电粒子在电场方向的偏转位移为电场宽度的一半,当粒子从磁场右边界上C点穿出磁场时速度方向与进入电场O点时的速度方向一致,已知d、v0(带电粒子重力不计),求:
(1)粒子从C点穿出磁场时的速度大小v.
(2)电场强度E和磁感应强度B的比值E/B.
在某空间存在着水平向右的匀强电场和垂直于纸面向里的匀强磁场,如图所示,一段光滑且绝缘的圆弧轨道AC固定在纸面内,其圆心为O点,半径R=1.8 m,OA连线在竖直方向上,AC弧对应的圆心角θ=37°.今有一质量m=3.6×10-4 kg,电荷量q=+9.0×10-4C的带电小球(可视为质点),以v0="4.0" m/s的初速度沿水平方向从A点射入圆弧轨道内,一段时间后从C点离开,小球离开C点后做匀速直线运动.已知重力加速度g="10" m
m,OA连线在竖直方向上,AC弧对应的圆心角θ=37°.今有一质量m=3.6×10-4 kg,电荷量q=+9.0×10-4C的带电小球(可视为质点),以v0="4.0" m/s的初速度沿水平方向从A点射入圆弧轨道内,一段时间后从C点离开,小球离开C点后做匀速直线运动.已知重力加速度g="10" m /s2,sin 37°=0.6,不计空气阻力,求:
/s2,sin 37°=0.6,不计空气阻力,求:
(1)匀强电场的场强E.
(2)小球射入圆弧轨道后的瞬间对轨道的压力.

光滑导轨MN, 竖直放置在垂直于纸面向里的匀强磁场中,已知导轨宽L=0 .5m,磁感应强度B=0.2T.有阻值为0.5Ω的导体棒AB紧挨导轨,沿着导轨由静止开始下落,如图所示,设串联在导轨中的电阻R阻值为2Ω,其他部分的电阻及接触电阻均不计.问:
.5m,磁感应强度B=0.2T.有阻值为0.5Ω的导体棒AB紧挨导轨,沿着导轨由静止开始下落,如图所示,设串联在导轨中的电阻R阻值为2Ω,其他部分的电阻及接触电阻均不计.问:
(1)导体棒AB在下落过程中,产生的感应电流的方向和AB棒受到的磁场力的方向.
(2)当导体棒AB的速度为5m/s(设并未达到最大速度)时,其感应电动势和感应电流的大小各是多少?
如图所示,在真空中有一与x轴平行的匀强电场,一电子由坐标原点O处以速度v0沿y轴正方向射入电场,在运动中该电子通过位于xoy平面内的A点,A点与原点O相距L,OA与x轴方向的夹角为θ,已知电子电量q = -1.6×10-19C,电子质量m = 9×10-31kg,初速度v0 = 1×107m/s,O与A间距L = 10cm、θ= 30º。求匀强电场的场强大小和方向。