如图,在直角梯形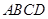 中,
中,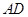 ∥
∥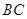 ,
,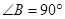 ,
,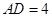 ,
,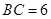 ,
,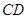 =
=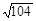 ,点
,点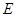 在
在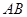 上,
上,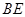 =4.
=4.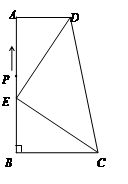
(1)线段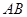 = ;
= ;
(2)试判断△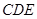 的形状,并说明理由;
的形状,并说明理由;
(3)现有一动点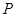 在线段
在线段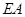 上从点
上从点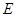 开始以每秒1个单位长度的速度向终点
开始以每秒1个单位长度的速度向终点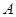 移动,设移动时间为
移动,设移动时间为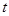 秒(
秒(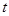 >0).问是否存在
>0).问是否存在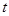 的值使得△
的值使得△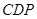 为直角三角形?若存在直接写出
为直角三角形?若存在直接写出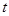 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知抛物线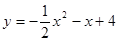 ,
,
(1)用配方法确定它的顶点坐标、对称轴;
(2)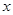 取何值时,
取何值时, 随
随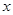 增大而减小?
增大而减小?
(3)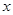 取何值时,抛物线在
取何值时,抛物线在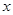 轴上方?
轴上方?
在△ABC中,AB=AC=5,BC=6,求cosB、sinA.
如图,已知O是坐标原点,B、C两点的坐标分别为(3,–1)、(2,1) .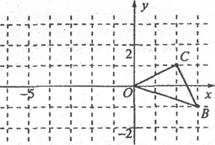
(1)以0点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;
(2)分别写出B、C两点的对应点B′、C′的坐标;
如图:已知△ABC为等腰直角三角形,∠ACB=90°,延长BA至E,延长AB至F,∠ECF=135°
求证:△EAC∽△CBF
清明节期间,某中学团委组织八年级部分学生去离校2.4千米的某烈士陵园扫墓,回来时乘公交车所花时间比去时步行少用了36分钟,已知公交车速度是学生步行速度的5倍,求学生的步行速度.