以原点O为圆心，1cm为半径的圆分别交
、
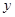轴的正半轴于A、B两点，点P的坐标为（2，0），动点Q从点B处出发，沿圆周按顺时针方向匀速运动一周，设运动的时间为秒.
（1）如图一，当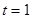
时，直线PQ恰好与⊙O第一次相切，连接OQ．求此时点Q的运动速度（结果保留
）；
（2）若点Q按照（1）中的速度继续运动.
①当为何值时，以O、P、Q为顶点的三角形是直角三角形；
②在①的条件下，如果直线PQ与⊙O相交，请求出直线PQ被⊙O所截的弦长.
如图，AB∥CD，直线EF分别交AB、CD于点E、F，EG平分∠AEF，∠1＝40°．求∠2的度数.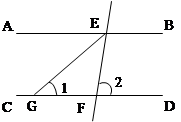
先化简，后求值：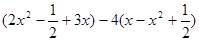
，其中
.
如左下图所示用5个棱长1厘米的小立方体块搭成的几何体，请画出它的主视图、俯视图与左视图.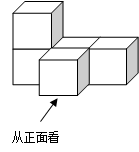
计算：
（1）（–2）2–（1–0.8×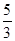
）÷（–2）
（2）
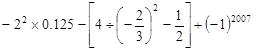
某校为了了解九年级学生的体能情况，抽调了一部分学生进行一分钟跳绳测试，将测试成绩整理后作出如下统计图．甲同学计算出前两组的频率和是0.12，乙同学计算出跳绳次数不少于100次的同学占96％，丙同学计算出从左至右第二.三.四组的频数比为4∶17∶15．结合统计图回答下列问题：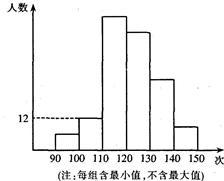
（1）这次共抽调了多少人?
（2）若跳绳次数不少于130次为优秀，则这次测试成绩的优秀率是多少?