如图,经过原点的抛物线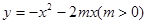 与
与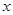 轴的另一个交点为A.过点
轴的另一个交点为A.过点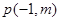 作直线
作直线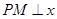 轴于点M,交抛物线于点B,过点B作直线BC∥
轴于点M,交抛物线于点B,过点B作直线BC∥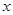 轴与抛物线交于点C(B、C不重合),连结CP.
轴与抛物线交于点C(B、C不重合),连结CP.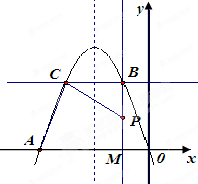
(1)当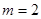 时,求点A的坐标及BC的长;
时,求点A的坐标及BC的长;
(2)当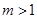 时,连结CA,问
时,连结CA,问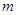 为何值时
为何值时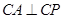 ?
?
(3)过点P作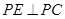 且
且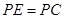 ,问是否存在
,问是否存在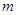 ,使得点E落在坐标轴上?若存在,求出所有满足要求的
,使得点E落在坐标轴上?若存在,求出所有满足要求的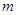 的值,并求出相对应的点E坐标;若不存在,请说明理由.
的值,并求出相对应的点E坐标;若不存在,请说明理由.
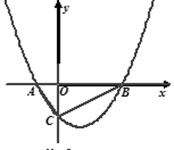
如图,抛物线y=x2-x+a与x轴交于点A,B,与y轴交于点C,其顶点在直线y=-2x上.求a的值;
求A,B的坐标;
以AC,CB为一组邻边作□ACBD,则点D关于x轴的对称点D′ 是否在该抛物线上?请说明理由.
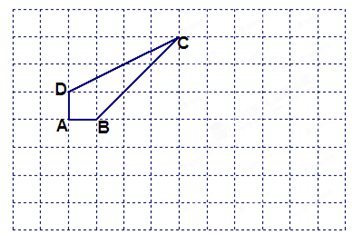
已知:如图,在8×12的矩形网格中,每个小正方形的边长都为1,四边形ABCD的顶点都在格点上.在所给网格中按下列要求画图:
在网格中建立平面直角坐标系(坐标原点为O),使四边形ABCD各个顶点的坐标分别为A(-5,0)、B(-4,0)、C(-1,3),D(-5,1);
将四边形ABCD沿坐标横轴翻折180°,得到四边形A’B’C’D’,再将四边形A’B’C’D’绕原点O旋转180°,得到四边形A”B”C”D”;写出C”、D”的坐标;
请判断四边形A”B”C”D”与四边形ABCD成何种对称?若成中心对称,请写出对称中心; 若成轴对称,请写出对称轴.
如图,已知抛物线y=ax2+bx+c经过 A(0,4),B(4,0),C(–1,0)三点.过点A作垂直于y轴的直线l. 在抛物线上有一动点P,过点P作直线PQ平行于y轴交直线l于点Q .连结AP.求抛物线y=ax2+bx+c的解析式;
是否存在点P,使得以A、P、Q三点构成的三角形与△AOC相似.如果存在,请求出点P的坐标,若不存在,请说明理由;
当点P位于抛物线y=ax2+bx+c的对称轴的右侧.若将△APQ沿AP对折,点Q的对应点为点M.求当点M落在坐标轴上时直线AP的解析式.

如图,△ABC内接于半圆,AB是直径,过A作直线MN,∠MAC=∠ABC,D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F.求证:MN是半圆的切线;
求证:FD=FG;
若△DFG的面积为4.5,且DG=3,GC=4,试求△BCG的面积.

“校园手机”现象越来越受到社会的关注﹒春节期间,小明随机调查了城区若干名同学和家长对中学生带手机现象的看法.统计整理并制作了如下的统计图:
这次的调查对象中,家长有 ▲ 人;
图②中表示家长“赞成”的圆心角的度数为 ▲ 度;
开学后,甲、乙两所学校对各自学校所有学生带手机情况进行了统计,发现两校共有384名学生带手机,且乙学校带手机的学生数是甲学校带手机学生数的,求甲、乙两校中带手机的学生数各有多少?