如图,在直三棱柱ABC—A1B1C1,AB=AC=1,∠BAC=90°,连结A1B与∠A1BC=60°.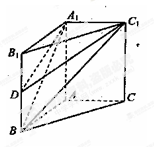
(Ⅰ)求证:AC⊥A1B;
(Ⅱ)设D是BB1的中点,求三棱锥D-A1BC1的体积.
设数列{an}是等差数列,数列{bn}的前n项和Sn满足 且
且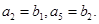
(Ⅰ)求数列{an}和{bn}的通项公式:
(Ⅱ)设Tn为数列{Sn}的前n项和,求Tn.
设正有理数x是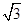 的一个近似值,令
的一个近似值,令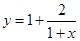 .
.
(Ⅰ)若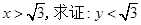 ;
;
(Ⅱ)比较y与x哪一个更接近于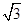 ,请说明理由.
,请说明理由.
在直角坐标系xOy中,圆C的参数方程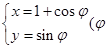 为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)直线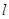 的极坐标方程是
的极坐标方程是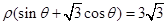 ,射线
,射线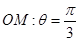 与圆C的交点为O,P,与直线
与圆C的交点为O,P,与直线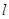 的交点为Q,求线段PQ的长.
的交点为Q,求线段PQ的长.
如图,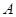 、
、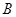 、
、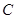 是圆
是圆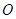 上三点,
上三点,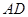 是
是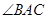 的角平分线,交圆
的角平分线,交圆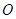 于
于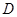 ,过
,过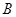 作圆
作圆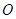 的切线交
的切线交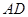 的 延长线于
的 延长线于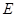 .
.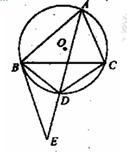
(Ⅰ)求证: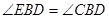 ;
;
(Ⅱ)求证: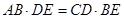 .
.