现有两个纸箱,每个纸箱内各装有4个材质、大小都相同的乒乓球,其中一个纸箱内4个小球上分别写有1、2、3、4这4个数，另一个纸箱内4个小球上分别写有5、6、7、8这4个数，甲、乙两人商定了一个游戏，规则是：从这两个纸箱中各随机摸出一个小球，然后把两个小球上的数字相乘，若得到的积是2的倍数，则甲得1分，若得到积是3的倍数，则乙得2分.完成一次游戏后,将球分别放回各自的纸箱,摇匀后进行下一次游戏,最后得分高者胜出.。
(1)请你通过列表(或树状图)分别计算乘积是2的倍数和3的倍数的概率;
(2)你认为这个游戏公平吗?为什么?若你认为不公平,请你修改得分规则,使游戏对双方公平.
若有理数x，y满足（x+1）2=16，|2y﹣1|=9，且|x+y|=﹣x﹣y，求3x+2y﹣xy的值．
甲骑摩托车，乙骑自行车从相距25km的两地相向而行．
（1）甲、乙同时出发经过0.5小时相遇，且甲每小时行驶路程是乙每小时行驶路程的3倍少6km，求乙骑自行车的速度．
（2）在甲骑摩托车和乙骑自行车与（1）相同的前提下，若乙先出发0.5小时，甲才出发，问：甲出发几小时后两人相遇？
如图AB=48，C为线段AB的延长线上一点，M，N分别是AC，BC的中点．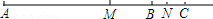
（1）若BC=10，求MN的长；
（2）若BC的长度为不定值，其它条件不变，MN的长还是定值吗？若是，请求出MN的长；若不是，请说明理由．
当x=﹣2时，代数式x3﹣2tx2+（1﹣t）x+t﹣1的值是﹣6，求当x=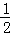
时该代数式的值．
如图，在同一个平面内有四个点A、B、C、D．
①画射线CD；②画直线AD；③连接AB；④直线BD与直线AC相交于点O．