如图,在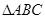 中
中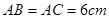 ,
,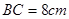 .点
.点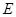 是线段
是线段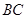 边上的一动点(不含
边上的一动点(不含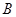 、
、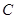 两端点),连结
两端点),连结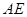 ,作
,作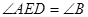 ,交线段
,交线段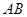 于点
于点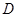 .
. 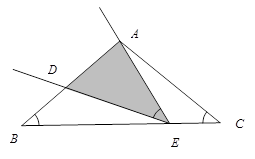
(1)求证: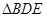 ∽
∽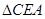 ;
;
(2)设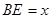 ,
,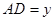 ,请写
,请写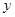 与
与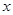 之间的函数关系式,并求
之间的函数关系式,并求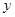 的最小值。
的最小值。
(3)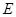 点在运动的过程中,
点在运动的过程中,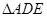 能否构成等腰三角形?若能,求出
能否构成等腰三角形?若能,求出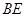 的长;若不能,请说明理由。
的长;若不能,请说明理由。
某工厂有一种材料,可加工甲、乙、丙三种型号机械配件共240件,厂方计划由20个工人一天内加工完成,并要求每人只加工一种配件,根据下表提供的信息,解答下列问题:
| 配件种类 |
甲 |
乙 |
丙 |
| 每人可加工配件的数量(个) |
16 |
12 |
10 |
| 每个配件获利(元) |
6 |
8 |
5 |
(1)设加工甲种配件的人数为x,加工乙种配件的人数为y,求y与x之间的函数关系式
(2)如果加工每种配件的人数均不少于3人,那么加工配件的人数安排方案有几种?并写出每种安排方案
(3)要使此次加工配件的利润最大,应采用哪种方案?最大利润是多少?
为了建设社会主义新农村,华新村修筑了一条长3000m的公路,实际工作效率比原计划提高了20%,结果提前5天完成任务。问原计划每天修路多长?
如图,一次函数图象与x轴交于点B,与反比例函数图象
交于点A(1,-6),△AOB的面积为6,求一次函数和反比例函 数的解析式
数的解析式
解方程组:
 |
先化简,再选择一个你喜欢的值代入求值: