某种产品的广告费支出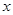 与销售额
与销售额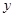 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
(1)画出散点图。
(2)求回归直线方程。
(3)试预测广告费支出为10百万元时,销售额多大
(本小题满分14分)
已知 有
有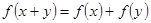
(1)判断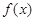 的奇偶性;
的奇偶性;
(2)若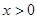 时,
时,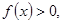 证明:
证明: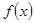 在
在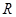 上为增函数;
上为增函数;
(3)在条件(2)下,若 ,解不等式:
,解不等式:
(本小题满分12分)
某地区对12岁儿童瞬时记忆能力进行调查.瞬时记忆能力包括听觉记忆能力与视觉记忆能力.某班学生共有40人,下表为该班学生瞬时记忆能力的调查结果.例如表中听觉记忆能力为中等,且视觉记忆能力偏高的学生为3人.
 视觉 视觉 |
视觉记忆能力 |
||||
| 偏低 |
中等 |
偏高 |
超常 |
||
| 听觉 记忆 能力 |
偏低 |
0 |
7 |
5 |
1 |
| 中等 |
1 |
8 |
3 |
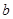 |
|
| 偏高 |
2 |
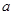 |
0 |
1 |
|
| 超常 |
0 |
2 |
1 |
1 |
由于部分数据丢失,只知道从这40位学生中随机抽取一个,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的概率为 .
.
(1)试确定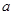 、
、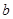 的值;
的值;
(2)从40人中任意抽取1人,求此人听觉记忆能力恰为中等,且视觉记忆能力为中等或中等以上的概率.
(本小题满分12分)
已知函数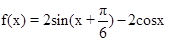 .
.
(Ⅰ)若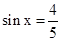 ,
,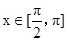 ,求函数f(x)的值; (Ⅱ)求函数f(x)的最小正周期和值域.
,求函数f(x)的值; (Ⅱ)求函数f(x)的最小正周期和值域.
已知⊙ 的半径是
的半径是 , 它的内接三角形
, 它的内接三角形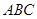 中, 有
中, 有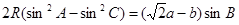 成立,求角
成立,求角 的大小及三角形面积
的大小及三角形面积 的最大值.
的最大值.
已知 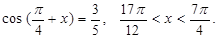
(1) 求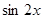 的值. (2) 求
的值. (2) 求  的值.
的值.