已知坐标平面上点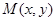 与两个定点
与两个定点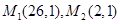 的距离之比等于5.
的距离之比等于5.
(1)求点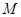 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;
(2)记(1)中的轨迹为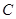 ,过点
,过点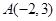 的直线
的直线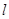 被
被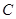 所截得的线段的长为8,求直线
所截得的线段的长为8,求直线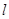 的方程
的方程
根据空气质量指数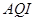 (为整数)的不同,可将空气质量分级如下表:
(为整数)的不同,可将空气质量分级如下表:
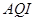 (数值) (数值) |
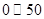 |
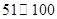 |
 |
 |
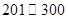 |
 |
| 空气质量级别 |
一级 |
二级 |
三级 |
四级 |
五级 |
六级 |
| 空气质量类别 |
优 |
良 |
轻度污染 |
中度污染 |
重度污染 |
严重污染 |
| 空气质量类别颜色 |
绿色 |
黄色 |
橙色 |
红色 |
紫色 |
褐红色 |
某市2013年10月1日—10月30日,对空气质量指数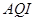 进行监测,获得数据后得到如图的条形图:
进行监测,获得数据后得到如图的条形图: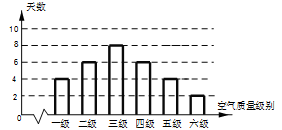
(1)估计该城市本月(按30天计)空气质量类别为中度污染的概率;
(2)在上述30个监测数据中任取2个,设 为空气质量类别颜色为紫色的天数,求
为空气质量类别颜色为紫色的天数,求 的分布列.
的分布列.
在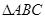 中,角
中,角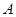 、
、 、
、 的对边分别为
的对边分别为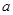 、
、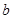 、
、 ,且
,且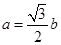 ,
,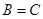 .
.
(1)求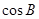 的值;
的值;
(2)设函数 ,求
,求 的值.
的值.
已知等差数列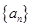 的首项
的首项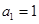 ,公差
,公差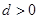 ,且其第二项、第五项、第十四项分别是等比数列
,且其第二项、第五项、第十四项分别是等比数列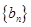 的第二、三、四项.
的第二、三、四项.
(1)求数列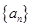 与
与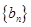 的通项公式;
的通项公式;
(2)令数列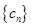 满足:
满足: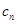 =
= ,求数列
,求数列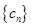 的前101项之和
的前101项之和 ;
;
(3)设数列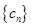 对任意
对任意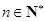 ,均有
,均有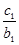 +
+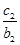 + +
+ +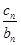 =
= 成立,求
成立,求 的值.
的值.
如图,边长为2的正方形 所在的平面与平面
所在的平面与平面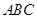 垂直,
垂直,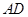 与
与 的交点为
的交点为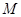 ,
, 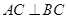 ,且
,且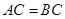 .
.
(1)求证: 平面
平面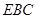 ;
;
(2)求直线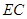 与平面
与平面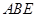 所成线面角的正切值.
所成线面角的正切值.
在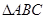 中,角
中,角 为锐角,已知内角
为锐角,已知内角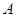 、
、 、
、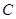 所对的边分别为
所对的边分别为 、
、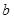 、
、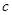 ,向量
,向量 且向量
且向量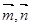 共线.
共线.
(1)求角 的大小;
的大小;
(2)如果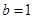 ,且
,且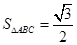 ,求
,求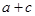 的值.
的值.