下表提供了某工厂节能降耗技术改造后生产甲产品过程中记录的产量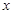 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨标准煤)的几组对照数据。
(吨标准煤)的几组对照数据。
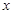 |
3 |
4 |
5 |
6 |
 |
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出 关于
关于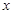 的线性回归方程
的线性回归方程 ;
;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤。试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
已知函数f(x)=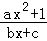 (a,b,c∈Z)是奇函数,且f(1)=2,f(2)<3.
(a,b,c∈Z)是奇函数,且f(1)=2,f(2)<3.
(1)求a,b,c的值.
(2)判断函数f(x)在[1,+∞)上的单调性,并用定义证明你的结论.
(3)解关于t的不等式:f(﹣t2﹣1)+f(|t|+3)>0.
电信局为了配合客户不同需要,设有A,B两种优惠方案.这两种方案应付话费(元)与通话时间x(min)之间的关系如图所示,其中D的坐标为( ,230).
,230).
(1)若通话时间为2小时,按方案A,B各付话费多少元?
(2)方案B从500分钟以后,每分钟收费多少元?
(3)通话时间在什么范围内,方案B比方案A优惠?
已知函数f(x)是定义域在R上的奇函数,当x>0时,f(x)=x2﹣2x.
(1)求出函数f(x)在R上的解析式;
(2)写出函数的单调区间.
已知集合M={x|x2﹣3x≤10},N={x|a+1≤x≤2a+1}.
(1)若a=2,求M∩(∁RN);
(2)若M∪N=M,求实数a的取值范围.
(1)若xlog32=1,试求4x+4﹣x的值;
(2)计算:(2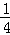 )
) ﹣(﹣9.6)0﹣(3
﹣(﹣9.6)0﹣(3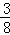 )
)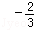 +(1.5)﹣2+(
+(1.5)﹣2+(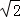 ×
×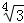 )4.
)4.