如图所示,真空管内的阴极K发出的电子(不计初速、重力和电子间的相互作用)经加速电压U1加速后,穿过AA'中心的小孔沿中心轴O1 O的方向进入到两块水平正对放置的平行极板P和P'间的区域.当极板P和P'间不加偏转电压时,电子束打在荧光屏的中心O点处,形成了一个亮点;若加上偏转电压U2后,亮点则偏离到O'点.已知电子带电量为-e、质量为m,极板P和P'水平方向的长度为L、极板间距为b,极板右端到荧光屏的距离可忽略不计(如图所示) .求: 
(1)打在荧光屏O点的电子速度的大小
(2)荧光屏上O'点与O点的竖直间距多大
跳伞运动员从480 m的高空离开直升飞机,自由下落一段距离后达到最大速度则打开伞,设开伞后以2 m/s2的加速度做匀减速直线运动,到达地面时速度刚好为零,求他下落的总时间及自由下落的距离.(g=10 m/s2)
某人造地球卫星沿圆轨道运行,轨道半径是r,周期是T。试根据这些量推导出计算地球质量M的表达式。(引力常量为G)
一物体在水平面内沿半径 R=" 0.20" m的圆形轨道做匀速圆周运动,线速度V=0.2m/s,试求:(1)它的向心加速度为多少m/s2?(2)它的角速度为多少 rad/s?
从某高度处以12m/s的初速度水平抛出一物体,经2s 落地,g取10m/s2,试求:(1)物体抛出处的高度是多少m?(2)物体的水平位移是多少m?
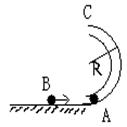
如图所示,半径为R、内径很小的光滑半圆管置于竖直平面内,两个质量均为m的小球A、B,以不同的速度进入管内,A通过最高点C时,对管壁上部的压力为3mg,B通过最高点C时,对管壁下部的压力为0.75mg,求A、B两球落地点间的距离。