如图,在Rt△ABC中,∠ACB=90°,AC=9cm,BC=12cm,P为BC的中点.动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.
(1)求点P到直线AB的距离;
(2)当t=1.8时,判断直线AB与⊙P的位置关系,并说明理由;
(3)已知⊙O为△ABC的外接圆,若⊙P与⊙O相切,求t的值.
某联欢会上有一个有奖游戏,规则如下:有5张纸牌,背面都是喜羊羊头像,正面有2张是笑脸,其余3张是哭脸.现将5张纸牌洗匀后背面朝上摆放到桌上,若翻到的纸牌中有笑脸就有奖,没有笑脸就没有奖.
(1)小芳获得一次翻牌机会,她从中随机翻开一张纸牌.小芳得奖的概率是.
(2)小明获得两次翻牌机会,他同时翻开两张纸牌.小明认为这样得奖的概率是小芳的两倍,你赞同他的观点吗?请用树形图或列表法进行分析说明.
如图,在菱形ABCD中,∠A=60°,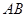 =4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.
=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.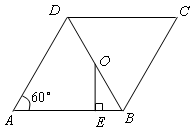
(1) 求∠ABD的度数; (2)求线段 的长.
的长.
某市“每天锻炼一小时,幸福生活一辈子”活动已开展了一年,为了解该市此项活动的开展情况,某调查统计公司准备采用以下调查方式中的一种进行调查:
A.从一个社区随机选取200名居民;
B.从一个城镇的不同住宅楼中随机选取200名居民;
C.从该市公安局户籍管理处随机抽取200名城乡居民作为调查对象,然后进行调查.
(1)在上述调查方式中,你认为比较合理的一个是(填番号).
(2)由一种比较合理的调查方式所得到的数据制成了如图所示的频数分布直方图,在这个调查中,这200名居民每天锻炼2小时的人数是多少?
(3)若该市有l00万人,请你利用(2)中的调查结果,估计该市每天锻炼2小时及以上的人数是多少?
(4)你认为这个调查活动的设计有没有不合理的地方?谈谈你的理由.
先化简,再求代数式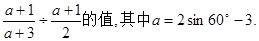
①(2010四川眉山)解方程: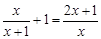
②(2010浙江嘉兴)解方程: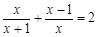 .
.