已知过抛物线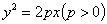 的焦点,斜率为
的焦点,斜率为 的直线交抛物线于
的直线交抛物线于
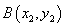 (
( )两点,且
)两点,且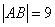 .
.
(1)求该抛物线的方程;
(2) 为坐标原点,
为坐标原点,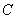 为抛物线上一点,若
为抛物线上一点,若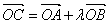 ,求
,求 的值.
的值.
设集合 ,
, 。
。
(1)当 时,求
时,求 的非空真子集的个数;
的非空真子集的个数;
(2)若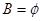 ,求
,求 的取值范围;
的取值范围;
(3)若 ,求
,求 的取值范围。
的取值范围。
设 x1、x2( )是函数
)是函数  (
(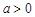 )的两个极值点.
)的两个极值点.
(I)若  ,
,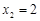 ,求函数
,求函数 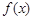 的解析式;
的解析式;
(II)若  ,求 b 的最大值;
,求 b 的最大值;
已知三次函数 的导函数
的导函数 ,
, ,
,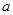 、
、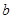 为实数。
为实数。
(Ⅰ)若曲线
 在点(
在点( ,
,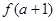 )处切线的斜率为12,求
)处切线的斜率为12,求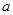 的值;
的值;
(Ⅱ)若 在区间[-1,1]上的最小值、最大值分别为-2、1,且
在区间[-1,1]上的最小值、最大值分别为-2、1,且 ,求函数
,求函数 的解析式。
的解析式。
数列 满足
满足
 .
.
(Ⅰ)若 是等差数列,求其通项公式;
是等差数列,求其通项公式;
(Ⅱ)若 满足
满足 ,
,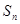 为
为 的前
的前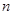 项和,求
项和,求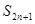 .
.
已知向量  与
与 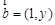 共线,设函数
共线,设函数  。
。
(1)求函数 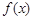 的周期及最大值;
的周期及最大值;
(2)已知锐角 △ABC 中的三个内角分别为 A、B、C,若有  ,边 BC=
,边 BC= ,
,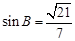 ,求 △ABC 的面积.
,求 △ABC 的面积.