据交管部门统计，高速公路超速行驶是引发交通事故的主要原因．我市某校数学课外小组的几个同学想尝试用自己所学的知识检测车速，甬台温高速公路温州—瑞安路段的限速是：每小时80千米（即最高时速不超过80千米），如图，他们将观测点设在离公路L的距离为0.1千米的P处．这时，一辆轿车由温州向瑞安匀速直线驶来，测得此车从A处行驶到B处所用的时间为3秒，并测得∠APO＝60°，∠BPO＝45°．试计算AB的长度并判断此车是否超速？
解方程：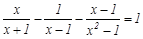
.
计算：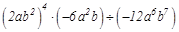
.
（本小题8分）如图，已知点A、B、C是数轴上三点，点C表示的数为6，BC＝4，AB＝12．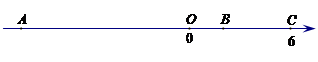
（1）数轴上点A表示的数是，点B表示的数是；
（2）动点P、Q同时从A、C出发，点P以每秒6个单位长度的速度沿数轴向右匀速运动，点Q以3个单位长度的速度沿数轴向左匀速运动，M为AP的中点， N在线段CQ上，且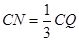
，设运动时间为t（t>0）秒．
①求数轴上点M、N表示的数（用含t的式子表示）；
②t为何值时，原点O恰为线段PQ的中点．
（本小题8分）小学毕业时，六年级某班为纪念师生情谊，班委决定花800元班费买两种不同单价的留念册，分别给50位同学和10位任课老师每人一本留做纪念。其中送给任课老师的留念册的单价比给同学的单价多8元。请问这两种不同留念册的单价分别为多少元？
（本小题6分）如图，有一个形如六边形的点阵，它的中心是一个点，算第一层，第二层每边有两个点，第三层每边有三个点，依次类推．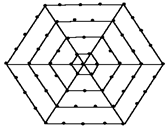
（1）写出第n层所对应的点数．
（2）如果某一层共96个点，你知道它是第几层吗？
（3）写出n层的六边形点阵的总点数．