已知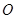 是
是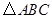 所在平面内一点,
所在平面内一点, 为
为 边中点,且
边中点,且 ,那么( )
,那么( )
A. |
B. |
C. |
D.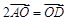 |
设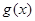 是将函数
是将函数 向左平移
向左平移 个单位得到的,则
个单位得到的,则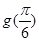 等于
等于
A. |
B. |
C. |
D. |
为了了解某校今年准备报考飞行员的学生的体重情况,将所得的数据整理后,画
出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1∶2∶3,第1
小组的频数为6,则报考飞行员的学生人数是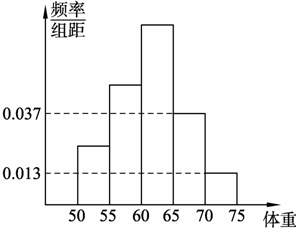
| A.36 | B.40 | C.48 | D.50 |
函数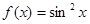 是
是
A.最小正周期为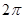 的奇函数 的奇函数 |
B.最小正周期为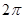 的偶函数 的偶函数 |
C.最小正周期为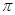 的奇函数 的奇函数 |
D.最小正周期为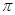 的偶函数 的偶函数 |
某校五四演讲比赛中,七位评委为一选手打出的分数如下:90 86 90 97 93 94 93 去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为
A.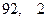 |
B.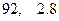 |
C.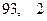 |
D.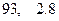 |
下列命题正确的个数是
①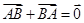 ;②
;②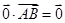 ;③
;③ ;④
;④
| A.1 | B.2 | C.3 | D.4 |