某同学通过以下步骤测出了从一定髙度落下的排球对地面的冲击力:将一张白纸铺在水平地面上,把排球在水里弄湿,然后让排球从规定的高度自由落下,并在白纸上留下球的水印。再将印有水印的白纸铺在台秤上,将球放在纸上的水印中心,缓慢地向下压球,使排球与纸接触部分逐渐发生形变直至刚好遮住水印,记下此时台秤的示数,然后根据台秤的示数算出冲击力的最大值。该同学所用的研究方法(或思想)是
| A.等效替代 | B.极限思想 | C.比值定义 | D.理想化模型 |
半圆柱体P放在粗糙的水平地面上,其右端有固定放置的竖直挡板MN,在P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于静止状态,如图所示是这个装置的截面图,若用外力使MN保持竖直且缓慢地向右移动,在Q落到地面以前,发现P始终保持静止,在此过程中,下列说法中正确的是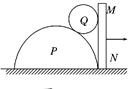
| A.MN对Q的弹力逐渐减小 | B.地面对P的摩擦力逐渐增大 |
C.P、Q间的 弹力先减小后增大 弹力先减小后增大 |
D.Q所受的合力逐渐增大 |
火车轨道在转弯处外轨高于内轨,且高度差由转弯半径与火车速度确定。若在某转弯处规定行驶速度为v,则下列说法中正确的是
①当以v的速度通过此弯路时,火车重力与轨道面支持力的合力提供向心力
②当以v的速度通过此弯路时,火车重力、轨道面支持力和外轨对轮缘弹力的合力提供向心力
③当速度大于v时,轮缘挤压外轨
④当速度小于v时,轮缘挤压外轨
| A.①③ | B.①④ | C.②③ | D.②④ |
物体以v0的速度水平抛出,忽略空气阻力,重力加速度为g, 当其竖直分位移与水平分位移大小相等时,下列说法中正确的是
| A.竖直分速度与水平分速度大小相等 |
B.瞬时速度的大小为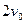 |
C.运动时间为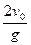 |
| D.瞬时速度方向与水平方向成450角斜向下 |
一小石块从空中a点自由落下,先后经过b点和c点,不计空气阻力。经过b点时速度为v,经过c点时速度为3v,则ab段与ac段位移之比为
| A.1∶3 | B.1∶5 | C.1∶8 | D.1∶9 |
宇宙飞船运动中需要多次“轨道维持”。所谓“轨道维持”就是通过控制飞船上发动机的点火时间和推力的大小和方向,使飞船能保持在预定轨道上稳定运行。如果不进行“轨道维持”,由于飞船受轨道上稀薄空气的影响,轨道高度会逐渐降低,在这种情况下飞船的动能、引力势能和机械能的变化情况将会是
| A.动能、重力势能和机械能逐渐减小 |
| B.重力势能逐渐减小,动能逐渐增大,机械能不变 |
| C.重力势能逐渐增大,动能逐渐减小,机械能不变 |
| D.重力势能逐渐减小,动能逐渐增大,机械能逐渐减小 |