已知：如图，在平面直角坐标系
O
中，矩形OABC的边OA在轴的正半轴上，OC在轴的正半轴上，OA=2，OC=3.过原点O作∠AOC的平分线交AB于点D，连接DC，过点D作DE⊥DC，交OA于点E.
（1）求过点E、D、C的抛物线的解析式；
（2）将∠EDC绕点D按顺时针方向旋转后，角的一边与轴的正半轴交于点F，另一边与线段OC交于点G.如果DF与（1）中的抛物线交于另一点M，点M的横坐标为
，那么EF=2GO是否成立？若成立，请给予证明；若不成立，请说明理由；
（3）对于（2）中的点G，在位于第一象限内的该抛物线上是否存在点Q，使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形？若存在，请求出点Q的坐标；若不存在，请说明理由.
（本小题满分8分）
如图，在△ABC中，D是AC的中点，E是线段BC延长线上一点，过点A作BE的平行线AF与线段ED的延长线交予点F，连接AE，EF．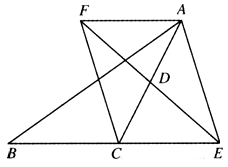
（1）求证：AF=CE；
（2）如果AC=EF，且∠ACB=135°,试判断四边形AFCE是什么样的四边形，并证明你的结论．
（本小题满分8分）
某学校组织八年级学生参加社会实践活动，若单独租用35座客车若干辆，则刚好坐满；若单独租用55座客车，则可以少租一辆，且余45个空座位．
（1）求该校八年级学生参加社会实践活动的人数；
（2）已知35座客车的租金为每辆320元，55座客车的租金为每辆400元．根据租车资金不超过1 500元的预算，学校决定同时租用这两种客车共4辆（可以坐不满）．
请你计算本次社会实践活动所需车辆的租金．
（本小题满分8分）
已知一次函数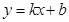
的图象与直线
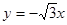平行且经过点（2，
），与
轴、
轴分别交于A，B两点．
（1）求此一次函数的解析式；
（2）过坐标原点O作OC⊥AB交AB于点C，求OC的长．
（本小题满分7分）
如图，小明站在A处放风筝，风筝飞到C处时的线长为20米，这时测得∠CBD=60°，若牵引底端AB离地面1．5米，求此时离地面高度．（计算结果精确到0．1米，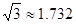
（本小题满分7分）解方程：