如图所示，是磁流体动力发电机的工作原理图．一个水平放置的上下、前后封闭的矩形塑料管，其宽度为a，高度为b，其内充满电阻率为ρ的水银，由涡轮机产生的压强差p使得这个流体具有恒定的流速v0．管道的前后两个侧面上各有长为L的由铜组成的面，实际流体的运动非常复杂，为简化起见作如下假设：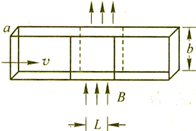
a.尽管流体有粘滞性，但整个横截面上的速度均匀；
b.流体的速度总是与作用在其上的合外力成正比；
c.导体的电阻：R=ρl／S，其中ρ、l和S分别为导体的电阻率、长度和横截面积；
d.流体不可压缩．
若由铜组成的前后两个侧面外部短路，一个竖直向上的匀强磁场只加在这两个铜面之间的区域，磁感强度为B（如图）．
(1)写出加磁场后，两个铜面之间区域的电阻R的表达式
(2)加磁场后，假设新的稳定速度为v，写出流体所受的磁场力F与v关系式，指出F的方向
(3)写出加磁场后流体新的稳定速度v的表达式（用v0、p、L、B、ρ表示）；
(4)为使速度增加到原来的值v0，涡轮机的功率必须增加，写出功率增加量的表达式（用v0、a、b、L、B和ρ表示）。
质量均为m的三个星球A、B、C分别位于边长为L的等边三角形的三个顶点上，它们在彼此间万有引力的作用下，沿等边三角形的外接圆作匀速圆周运动，运动中三个星球始终保持在等边三角形的三个顶点上，求星球运动的周期。
如图所示，物体A、B用细线连接绕过定滑轮，物体C中央有开口，C放在B上。固定挡板D中央有孔，物体B可以穿过它而物体C又恰好能被挡住。物体A、B、C的质量MA＝0.80kg、MB＝MC＝0.10kg，物体B、C一起从静止开始下降H1＝0.50m后，C被固定挡板D截住，B继续下降H2＝0.30m后停止。求：物体A与平面的动摩擦因数μ（g=10m/s2） 
一物体由斜面顶端由静止开始匀加速下滑，最初的3秒
内的位移为x1，最后3秒内的位移为x2，若x2 —x1=6m，x1∶x2=3∶7，求斜面的长度为多少？
鸵鸟是当今世界上最大的鸟。有人说，如果鸵鸟能长出一副与身体大小成比例的翅膀，就能飞起来。是不是这样呢？
生物物理学家认为：鸟煽动翅膀，获得上举力的大小可以表示为F=kSv2，式中S为翅膀展开后的面积，v为鸟的飞行速度，而k是一个比例常数。
课题研究组的同学作一个简单的几何相似形假设：设鸟的几何线度为L，那么其质量m∝L3，而翅膀面积S∝L2，已知小燕子的最小飞行速度是5.5m/s，鸵鸟的最大奔跑速度为11.5m/s，又测得鸵鸟的体长是小燕子的25
倍，那么鸵鸟真的长出一副与身体大
小成比例的翅膀后能飞起来吗？
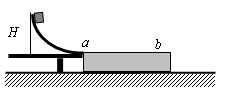
如图所示，光滑圆弧斜槽固定在台面上，一质量为m的小滑块，从斜槽上端比台面高H处由静止下滑，又滑到在台面旁固定的木块上，在木块上表面滑过s后，停在木块上，木块长为L，质量为M，求：
（1）小滑块滑到斜槽底端时的速度。
（2）小滑块与木块的动摩擦因数。
（3）若木块不固定，能沿光滑水平面运动，欲使小滑块在木块上恰滑到b端，且不掉下，小滑块应从距台面多高处由静止开始滑下。