如图,四棱锥 中,底面
中,底面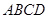 是边长为2的正方形,
是边长为2的正方形, ,且
,且 ,
, 为
为 中点.
中点.
(Ⅰ)求证: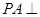 平面
平面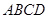 ;
;
(Ⅱ)求二面角 的大小;
的大小;
(Ⅲ)在线段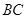 上是否存在点
上是否存在点 ,使得点
,使得点 到平
到平
面 的距离为
的距离为 ?若存在,确定点
?若存在,确定点 的位置;
的位置;
若不存在,请说明理由.
.(本题12分)已知函数 ,
,
(1)对任意的 ,若
,若 恒成立,求m取值范围;
恒成立,求m取值范围;
(2)对 ,
, 有两个不等实根,求m的取值范围.
有两个不等实根,求m的取值范围.
.(本题12分)已知函数
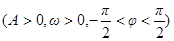 的图象与x轴交点为
的图象与x轴交点为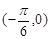 ,相邻最高点坐标为
,相邻最高点坐标为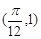 .
.
(1)求函数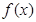 的表达式;
的表达式;
(2)求函数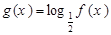 的单调增区间;
的单调增区间;
(3)求函数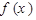 在
在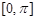 上的最值.
上的最值.
(本题12分)投掷一个质地均匀,每个面上标有一个数字的正方体玩具,它的六个面中,有两个面的数字是 ,两个面的数字是2,两个面的数字是4.将此玩具连续抛掷两次,以两次朝上一面出现的数字分别作为点P的横坐标和纵坐标.
,两个面的数字是2,两个面的数字是4.将此玩具连续抛掷两次,以两次朝上一面出现的数字分别作为点P的横坐标和纵坐标.
(1)求点P落在区域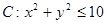 上的概率;
上的概率;
(2)若以落在区域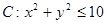 上的所有点为顶点作面积最大的多边形区域M,在区域C上随机撒一粒豆子,求豆子落在区域M上的概率.
上的所有点为顶点作面积最大的多边形区域M,在区域C上随机撒一粒豆子,求豆子落在区域M上的概率.
(本题12分)(1)求函数 的定义域
的定义域
(2)若 ,求
,求 的值.
的值.
(本题12分)某校从参加高一年级期中考试的学生中随机抽出60名学生,将其数学成绩(均为整数)分成六段[40,50)、[50,60)、…、[90,100)后得到如下部分频率分布直方图.
观察图形的信息,回答下列问题:(Ⅰ)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;
(Ⅲ)已知甲的考试成绩为45分,若从成绩在[40,60)的学生中随机抽取2人,求抽到学生甲的的概率.