 对任意
对任意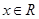 都有
都有
(Ⅰ)求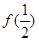 和
和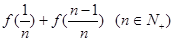 的值.
的值.
(Ⅱ)数列 满足:
满足: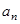 =
= +
+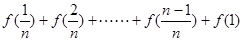 ,数列
,数列 是等差数列吗?请给予证明;
是等差数列吗?请给予证明;
(Ⅲ)令 试比较
试比较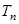 与
与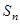 的大小.
的大小.
(本小题满分12分)
如图,在平面直角坐标系xOy中,平行于x轴且过点A(3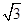 ,2)的入射光线 l1
,2)的入射光线 l1
被直线l:y=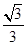 x反射.反射光线l2交y轴于B点,圆C过点A且与l1, l2都相切.
x反射.反射光线l2交y轴于B点,圆C过点A且与l1, l2都相切.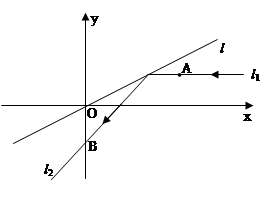
(1)求l2所在直线的方程和圆C的方程;
(2)设 分别是直线l和圆C上的动点,求
分别是直线l和圆C上的动点,求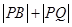 的最小值及此时点
的最小值及此时点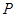 的坐标.
的坐标.
(本小题满分12分)
设圆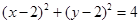 的切线
的切线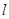 与两坐标轴交于点
与两坐标轴交于点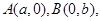
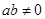 .
.
(1)证明: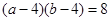 ;
;
(2)若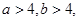 求△AOB的面积的最小值.
求△AOB的面积的最小值.
(本小题满分12分)
己知圆C: (x – 2 )2 + y 2 =" 9," 直线l:x + y = 0.
(1) 求与圆C相切, 且与直线l平行的直线m的方程;
(2) 若直线n与圆C有公共点,且与直线l垂直,求直线n在y轴上的截距b的取值范围;
(本小题满分12分)
命题p:对任意实数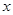 都有
都有 恒成立;命题q:关于
恒成立;命题q:关于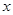 的方程
的方程 有实数根.若“p或q”为真命题,“p且q”为假命题,求实数
有实数根.若“p或q”为真命题,“p且q”为假命题,求实数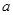 的取值范围。
的取值范围。
(本小题满分10分)
如图,在棱长为3的正方体 中,
中,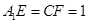 .
.
⑴求两条异面直线 与
与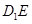 所成角的余弦值;
所成角的余弦值;
⑵求平面 与平面
与平面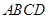 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.