如图所示,水平转台高h=1.25m,半径为R=0.2m,可绕通过竖直转轴转动。转台的同一半径上放有质量均为m=0.4kg的小物块A、B( 可视为质点),A与转轴间距离为r=0.1m,B位于转台边缘处,A、B间用长l=0.1m的细线相连,A、B与水平转台间最大静摩擦力均为fm=0.54N,g取10m/s2.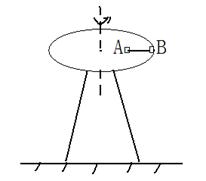
(1)当转台的角速度达到多大时细线上出现张力?
(2)当转台的角速度达到多大时A物体开始滑动?
(3)若A物体恰好将要滑动时细线断开,此后转台保持匀速转动,求B物块落地瞬间A、B两物块间的水平距离。(不计空气阻力,计算时取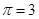 )
)
斜向上抛出一球,抛射角α=60°,当t=1秒时,球仍斜向上升,但方向已跟水平成β=45°角.(g取10 m/s2)
(1)球的初速度v0是多少?
(2)球将在什么时候达到最高点?
如图所示,细绳一端系着质量为M=0.6 kg的物体,静止在水平盘面上,另一端通过光滑小孔吊着质量m=0.3 kg的物体,M的中心与小孔距离为0.2 m,并知M和水平盘面的最大静摩擦力为2 N.现使此水平盘绕中心轴转动,问角速度ω在什么范围内m处于静止状态?(g取10 m/s2)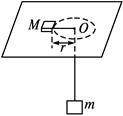
如图所示,有一质量为m的小球在光滑的半球形碗内做匀速圆周运动,轨道平面在水平面内.已知小球与半球形碗的球心O的连线跟竖直方向的夹角为θ,半球形碗的半径为R,求小球做圆周运动的速度及碗壁对小球的弹力各多大.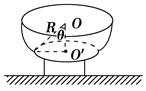
如图所示,质量相等的小球A、B分别固定在轻杆的中点及端点,当杆在光滑的水平面上绕O点匀速转动时,求杆的OA段及AB段对球的拉力大小之比.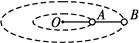
宇航员在地球表面以一定初速度竖直上抛一小球,经过时间t小球落回原处;若他在某星球表面以相同的初速度竖直上抛同一小球,需经过时间5t小球落回原处.(取地球表面重力加速度g=10 m/s2,空气阻力不计)
(1)求该星球表面附近的重力加速度g′;
(2)已知该星球的半径与地球半径之比为R星∶R地=1∶4,求该星球的质量与地球质量之比M星∶M地.