(1)如图(1)，在△ABC中，∠A=62°，∠ABD=20°，∠ACD=35°，求∠BDC的度数.
(2)图（1）所示的图形中，有像我们常见的学习用品——圆规。我们不妨把这样图形叫做“规形图”，观察“规形图”图（2）,试探究∠BDC与∠A、∠B、∠C之间的关系，并说明理由. 
（3）请你直接利用以上结论，解决以下问题：
如图(3)DC平分∠ ADB, EC平分∠AEB,若∠DAE=50°，∠DBE=130°，求∠DCE的度数. 
广珠城轨某路段需要铺轨．先由甲工程队独做2天后，再由乙工程队独做3天刚好完成这项任务．已知乙工程队单独完成这项任务比甲工程队单独完成这项任务多用2天，求甲、乙工程队单独完成这项任务各需要多少天？
目前世界上最高的电视塔是广州新电视塔“小蛮腰”，如图所示，新电视塔高AB为610米，远处有一栋大楼，某人在楼底C处测得塔顶B的仰角为45°，在楼顶D处测得塔顶B的仰角为39°．
求大楼与电视塔之间的距离AC；
求大楼的高度CD（精确到1米）．
（tan39°≈0.81，,cos39°≈0.78，,sin39°≈0.63）
如图，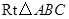
的斜边
，
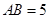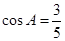．用尺规作图作线段
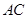的垂直平分线
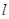（保留作图痕迹，不要求写作法、证明）；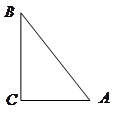
若直线
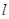与
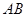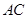，分别相交于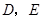
两点，求
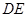的长
如图，点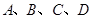
在同一条直线上，
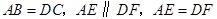，求证：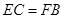
.
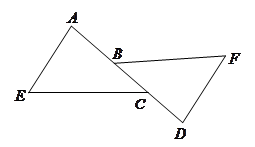
解不等式组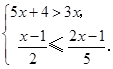
并把解集在数轴上表示出来．