如图所示，一列简谐横波沿x轴正方向传播。t=0时，波传播到x轴上的质点B，在它的左边质点A位于正的最大位移处，在t=0.6s时，质点A第二次出现在负的最大位移处。求：
（1）该波的周期T
（2）该波的波速v
（3）从t=0时开始到质点E第一次到达正向最大位移经历的时间及在该段时间内质点E通过的路程。
如图所示，长为L (L=ab=dc)，高为L(L=bc=ad)的矩形区域abcd内存在着匀强电场。电量为q、质量为m、初速度为
的带电粒子从a点沿ab方向进入电场，不计粒子重力。求：
（1）若粒子从c点离开电场，求电场强度的大小；
（2）若粒子从bc边某处离开电场时速度为
，求电场强度的大小。
如图所示，质量m=5.0×10-8kg的带电粒子，以初速v0=2m/s的速度从水平放置的平行金属板A、B的中央，水平飞入电场，已知金属板长0.1m，板间距离d=2×10-2m，当UAB=1000V时，带电粒子恰好沿直线穿过电场，若两极板间的电势差可调，要使粒子能从两板间飞出，UAB的变化范围是多少?（g取10m/s2）
如图所示，炽热金属丝上发射的电子（假设刚离开金属丝时的速度为0），经电压U1="4500" V加速后，以v0的速度垂直进入偏转电场，并能从偏转电场离开．偏转电场两极板间的电压U2="180" V，距离d="2" cm，板长L="8" cm.电子的质量m=0.9×10－30kg，电子的电荷量e=1.6×10－19C．求：
（1）v0的大小；
（2）电子在离开偏转电场时的纵向偏移量．
如图所示，一个质量m="30" g，带电荷量q=－1.5×10－8C的半径极小的小球，用绝缘丝线悬挂在水平方向的匀强电场中．当小球静止时，测得悬线与竖直方向成45°夹角．求：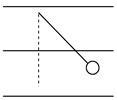
（1）小球受到的电场力的大小和方向；
（2）该电场的电场强度的大小和方向．
如图所示，无限宽广的匀强磁场分布在xoy平面内，x轴上下方磁场均垂直xoy 平面向里，x轴上方的磁场的磁感应强度为B，x轴下方的磁场的磁感应强度为4B/3。现有一质量为m，电量为-q带负电粒子以速度v0从坐标原点O沿y方向进入上方磁场。在粒子运动过程中，与x轴交于若干点。不计粒子的重力。求：
（1）粒子在x轴上方磁场做匀速圆周运动半径r1
（2）如把x轴上方运动的半周与x轴下方运动的半周称为一周期的话，则每经过一周期，在x轴上粒子右移的平均速度。
（3）在与x轴的所有交点中，粒子两次通过同一点的坐标位置。