如图所示，一绝缘轻绳绕过无摩擦的两轻质小定滑轮O1、O2，一端与质量m=0.2kg的带正电小环P连接，且小环套在绝缘的均匀光滑直杆上（环的直径略大于杆的截面直径），已知小环P带电q=4×10-5C，另一端加一恒定的力F=4N。已知直杆下端有一固定转动轴O，上端靠在光滑竖直墙上的A处，其质量M=1kg，长度L=1m，杆与水平面的夹角为θ=530，直杆上C点与定滑轮在同一高度，杆上CO=0.8m，滑轮O1在杆中点的正上方，整个装置在同一竖直平面内，处于竖直向下的大小E=5×104N/C的匀强电场中。现将小环P从C点由静止释放，求：（取g＝10m／s2）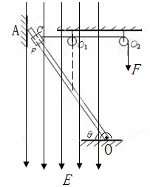
（1）刚释放小环时，竖直墙A处对杆的弹力大小；
（2）下滑过程中小环能达到的最大速度；
（3）若仅把电场方向反向，其他条件都不变，则环运动过程中电势能变化的最大值。
车在水平专用测试道上进行测试，该车总质量为m＝1×103 kg，由静止开始沿水平测试道运动．传感设备记录其运动的速度时间图象（v-t图象）如图所示．该车运动中受到的摩擦阻力（含空气阻力）恒定，且摩擦力与车对路面压力的比值为μ＝0．2．赛车在0～5 s的v-t图线为直线，5 s末达到该车发动机的额定牵引功率并保持该功率行驶，在5 s～50 s之间，赛车的v-t图线是一段曲线，50 s以后为直线．g取10 m/s2，
求：（1）该车发动机牵引力的额定功率P．
（2）该车行驶中的最大速度vm．
（3）该车出发后，前50 s内的位移x．
如图所示，滑雪运动员从一斜坡上的A处，从静止开始下滑到水平平台上的B处，然后继续向前滑行直至离开水平平台，最后落在水平地面上。已知h1 = 60m,h2=20m,滑雪运动员的质量为m=60kg，忽略一切摩擦和空气阻力，g取10m/s2。
求：（1）以水平平台为参考面，运动员开始下滑时的重力势能；
（2）运动员滑到斜坡底端B处时的速度大小；
（3）运动员离开平台后，在水平方向运动的距离。
一辆质量为0.40kg的遥控玩具车，从静止开始出发在平直轨道上行驶。已知发动机的牵引力为0.16N，玩具车在运动过程中受到的阻力为0.12N。求：
（1）玩具车在加速运动过程中的加速度大小
（2）玩具车开始加速运动6.0s内发生的位移
如图a所示，水平直线MN下方有竖直向上的匀强电场，现将一重力不计、比荷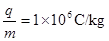
的正电荷置于电场中的O点由静止释放，经过
后，电荷以
的速度通过MN进入其上方的匀强磁场，磁场与纸面垂直，磁感应强度B按图b所示规律周期性变化（图b中磁场以垂直纸面向外为正，以电荷第一次通过MN时为t=0时刻）.
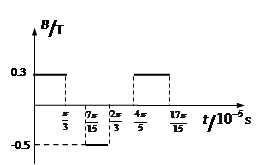
（1）求匀强电场的电场强度E；
（2）求图b中
时刻电荷与O点的水平距离；
（3）如果在O点右方d=68cm处有一垂直于MN的足够大的挡板，求电荷从O点出发运动到挡板所需的时间。
如图所示，电源的电动势E＝110 V，电阻R1＝21 Ω，电动机绕组的电阻R0＝0.5 Ω，电键S1始终闭合．当电键S2断开时，电阻R1的电功率是525 W；当电键S2闭合时，电阻R1的电功率是336 W，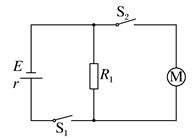
求：(1)电源的内电阻；
(2)当电键S2闭合时流过电源的电流
(3)当电键S2闭合时电动机的输出的功率．