某中学为了了解学生体育活动情况,随即调查了720名初二学生,调查内容是:“每天锻炼是否超过1小时及未超过1小时的原因”,利用所得的数据制成了扇形统计图和频数分布直方图.根据图示,解答下列问题:
(1)若在被调查的学生中随机选出一名学生测试其体育成绩,选出的是“每天锻炼超过1小时”的学生的概率是多少?
(2)“没时间”锻炼的人数是多少?并补全频数分布直方图;
(3)2012年宁波市区初二学生约为2万人,按此调查,可以估计2012年宁波市区初二学生中每天锻炼未超过1小时的学生约有多少万人?
(4)请根据以上结论谈谈你的看法.
(本题5分)有这样一道题:
“计算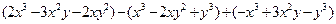 的值,其中
的值,其中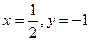 ”。甲同学把“
”。甲同学把“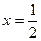 ”错抄成“
”错抄成“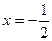 ”,但他计算的结果也是正确的,试说明理由,并求出这个结果.
”,但他计算的结果也是正确的,试说明理由,并求出这个结果.
(本题8分)把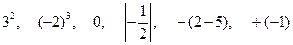 表示在数轴上,并将它们按从小到大的顺序排列
表示在数轴上,并将它们按从小到大的顺序排列
简答题(共2题,每小题3分,共6分)
(1)根据生活经验,对代数式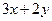 作出解释.
作出解释.
(2) 两个有理数的和是负数,那么这两个数一定都是负数,这种说法对吗?如果不对,请举例说明?
计算及化简: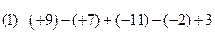
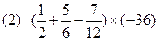
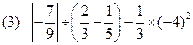
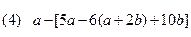
(本题12分)如图,在平面直角坐标系中,二次函数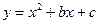 的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.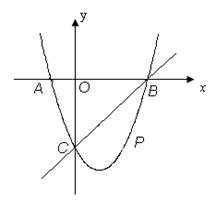
(1)求b,c的值.
(2)连结PO、PC,并把△POC沿CO翻折,得到四边形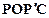 , 那么是否存在点P,使四边形
, 那么是否存在点P,使四边形 为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形 ABPC的面积最大,并求出此时P点的坐标和四边形ABPC的最大面积.