如甲图所示,水平光滑地面上用两颗钉子(质量忽略不计)固定停放着一辆质量为M=3kg的小车,小车的四分之一圆弧轨道是光滑的,半径为R=0.5m,在最低点B与水平轨道BC相切,视为质点的质量为m=1kg的物块从A点正上方距A点高为h=0.3m处无初速下落,恰好落入小车圆弧轨道滑动,然后沿水平轨道滑行恰好停在轨道末端C。
现去掉钉子(水平面依然光滑未被破坏)不固定小车,而让其左侧靠在竖直墙壁上,该物块仍从原高度处无初速下落,如乙图所示。
不考虑空气阻力和物块落入圆弧轨道时的能量损失,已知物块与水平轨道BC间的动摩擦因数为μ=0.2
求:(1)水平轨道BC长度;
(2)小车固定时物块到达圆弧轨道最低点B时对轨道的压力;
(3)小车不固定时物块再次停在小车上时距小车B点的距离;
(4)两种情况下由于摩擦系统产生的热量之比。
如图所示,在光滑的桌面上叠放着一质量为mA="2.0" kg的薄木板A和质量为mB="3" kg的金属块B.A的长度L="2.0" m.B上有轻线绕过定滑轮与质量为mC="1.0" kg的物块C相连.B与A之间的动摩擦因数μ=0.10,最大静摩擦力可视为等于滑动摩擦力.忽略滑轮质量及与轴间的摩擦.起始时令各物体都处于静止状态,绳被拉直,B位于A的左端(如图),然后放手,求经过多长时间后B从 A的右端脱离(设 A的右端距滑轮足够远)(取g="10" m/s2).
如图所示,高为h的车厢在平直轨道上匀减速向右行驶,加速度大小为a,车厢顶部A点处有油滴滴落到车厢地板上,车厢地板上的O点位于A点的正下方,则油滴落地点必在O点的左方还是右方?离O点距离为多少?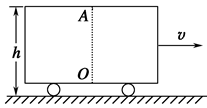
如图所示,在台秤上放半杯水,台秤示数为G′=50 N,另用挂在支架上的弹簧测力计悬挂一边长a=10 cm的金属块,金属块的密度ρ=13×103 kg/m3,当把弹簧测力计下的金属块平稳地浸入水深b=4 cm时,弹簧测力计和台秤的示数分别为多少?(水的密度是ρ水=103 kg/m3,g取10 m/s2)
有些人员,如电梯修理员、牵引专家等,常需要知道绳(或金属线)中的张力FT,可又不便到绳(或线)的自由端去测量.现某家公司制造了一种夹在绳上的仪表(图34中B、C为该夹子的横截面).测量时,只要如图示那样用一硬杆竖直向上作用在绳上的某点A,使绳产生一个微小偏移量a,借助仪表很容易测出这时绳对硬杆的压力F.现测得该微小偏移量为a=12 mm,BC间的距离为2L=250 mm,绳对横杆的压力为F=300 N,试求绳中的张力FT.
重500 N的物体放在水平地面上,物体与地面间的动摩擦因数为0.3.当用180 N的水平力推物体时,物体所受的摩擦力大小为多少?当用100 N的水平力推物体时,物体所受的摩擦力大小为多少?