(Ⅰ)设 ,求证:
,求证: ;
;
(Ⅱ)设 ,求证:三数
,求证:三数 ,
,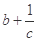 ,
, 中至少有一个不小于2.
中至少有一个不小于2.
如图,已知四棱锥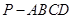 的底面
的底面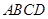 是菱形,
是菱形,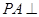 平面
平面 ,
,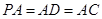 ,点
,点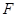 为
为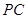 的中点.
的中点.
(Ⅰ)求证: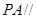 平面
平面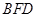 ;
;
(Ⅱ)求二面角 的正切值.
的正切值.
已知函数 在同一周期内有最高点
在同一周期内有最高点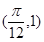 和最低点
和最低点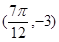 ,(1)求此函数
,(1)求此函数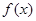 的解析式;(2)函数
的解析式;(2)函数 的图像如何由函数
的图像如何由函数 的图像变换得到?
的图像变换得到?
如图,从参加环保知识竞赛的学生中抽出 名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
(1)79.5到89.5这一组的频数、频率分别是多少?
(2)估计这次环保知识竞赛的及格率( 分及以上为及格).
分及以上为及格).
二次函数f(x)与g(x)=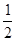 x2-1的图像开口大小相同,开口方向也相同,y=f(x)的对称轴方程为x=1,图像过点(2,
x2-1的图像开口大小相同,开口方向也相同,y=f(x)的对称轴方程为x=1,图像过点(2, 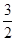 )点
)点
(1)求f(x)的解析式;
(2)是否存在大于1的实数m,使y=f(x)在[1, m]上的值域是[1, m]?若存在,求出m的值,若不存在,说明理由.
已知函数f(x)= , x∈[3, 5]
, x∈[3, 5]
(1)判断f(x)单调性并证明;
(2)求f(x)最大值,最小值.