如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距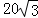 千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.
千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.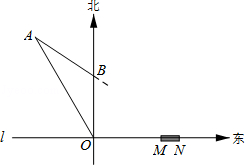
(1)求该轮船航行的速度;
(2)如果该轮船不改变航向继续航行,则轮船能否正好行至码头MN靠岸?请说明理由.
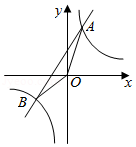
如图,在平面直角坐标系 中,已知一次函数 的图象与反比例函数 的图象相交于 , 两点,且点 的坐标为 .
(1)求该一次函数的解析式;
(2)求 的面积.
某校举办“创建全国文明城市”知识竞赛,计划购买甲、乙两种奖品共30件.其中甲种奖品每件30元,乙种奖品每件20元.
(1)如果购买甲、乙两种奖品共花费800元,那么这两种奖品分别购买了多少件?
(2)若购买乙种奖品的件数不超过甲种奖品件数的3倍.如何购买甲、乙两种奖品,使得总花费最少?
某汽车公司为了解某型号汽车在同一条件下的耗油情况,随机抽取了 辆该型号汽车耗油 所行使的路程作为样本,并绘制了如图不完整的频数分布直方图和扇形统计图.根据题中已有信息,解答下列问题:

(1)求 的值,并补全频数分布直方图;
(2)若该汽车公司有600辆该型号汽车.试估计耗油 所行使的路程低于 的该型号汽车的辆数;
(3)从被抽取的耗油 所行使路程在 , 这两个范围内的4辆汽车中,任意抽取2辆,求抽取的2辆汽车来自同一范围的概率.
化简: .
如图, 平分 , .求证: .
