如图，Rt△ABC中，∠ABC＝90°，以AB为直径的⊙O交AC于点D，E是BC的中点，连接DE、OE．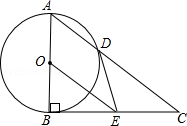
(1)判断DE与⊙O的位置关系并说明理由；
(2)若⊙O半径r=3，DE＝4，求AD的长．
如图，△ABC是⊙O的内接三角形，AC=BC，D为⊙O中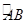
上一点，延长DA至点E，使CE=CD．
（1）求证：AE=BD；
（2）若AC⊥BC，求证：
．
（1）计算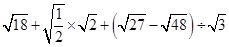
；
（2）已知，四边形ABCD顶点都在4×4正方形网格的格点上，如图所示，请用直尺和圆规画出四边形ABCD的外接圆，并标明圆心M的位置．这个圆中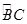
所对的圆心角的度数是．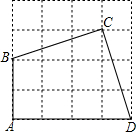
已知，如图，AD为△ABC的内角平分线，且AD=AB，CM⊥AD于M．求证：AM=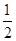
（AB+AC）．
某校初三（1）班进行立定跳远训练，以下是李超和陈辉同学六次的训练成绩（单位：m）
李超：2.50，2.42，2.52，2.56，2.48，2.58
陈辉：2.54，2.48，2.50，2.48，2.54，2.52
（1）李超和陈辉的平均成绩分别是多少？
（2）分别计算两人的六次成绩的方差，哪个人的成绩更稳定？为什么？
（3）若预知参加级的比赛能跳过2.55米就可能得冠军，应选哪个同学参加？为什么？
| 专项测试和6次跳远选拔赛成绩 |
平均数 |
方差 |
|||||||
| 李勇 |
603 |
589 |
602 |
596 |
604 |
612 |
608 |
602 |
|
| 张浩 |
597 |
580 |
597 |
630 |
590 |
631 |
596 |
333 |
某校要从新入学的两名体育特长生李勇、张浩中挑选一人参加校际跳远比赛，在跳远专项测试以及以后的6次跳远选拔赛中，他们的成绩（单位：cm）如下表所示：
（1）求张浩同学7次测试成绩的平均数，李勇同学7次测试成绩的方差；
（2）请你分别从平均数和方差的角度分析两人成绩的特点；
（3）经查阅历届比赛的资料，成绩若达到6.00m，就很可能得到冠军，你认为应选谁去参赛夺冠军比较有把握？说明理由；
（4）以往的该项最好成绩的纪录是6.15m，若要想打破纪录，你认为应选谁去参赛？