已知三棱锥S－ABC的所有顶点都在球O的球面上，SA⊥平面ABC，SA=2
，AB=1，AC=2，∠BAC=60°，则球O的表面积为
A．4 |
B．12 |
C．16 |
D．64 |
已知两定点F1(-5,0)、F2(5,0),动点P满足|PF1|-|PF2|=2a,则当a=3或a=5时,P点的轨迹为( )
| A．双曲线和一条直线 |
| B．双曲线和一条射线 |
| C．双曲线的一支和一条射线 |
| D．双曲线的一支和一条直线 |
已知方程
=1表示双曲线，则k的取值范围是( )
| A．-1＜k＜1 | B．k＞0 |
| C．k≥0 | D．k＞1或k＜-1 |
P为双曲线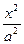
-
=1(a>0,b>0)上的一点,F1、F2为焦点,若∠F1PF2=60°,则
等于( )
A． b2 |
B． ab |
C． |b2-a2| |
D． (a2+b2) |
已知△ABC的顶点A(0,-4)、B(0,4),且4(sinB-sinA)=3sinC,则顶点C的轨迹方程是( )
A.
-
="1(x>3)" B.
-
=1(x<-7)
C.-="1(y>3)" D.-=1(y<-3)
若
+
=-1表示焦点在y轴上的双曲线,则它的半焦距c的取值范围是( )
| A．(1,+∞) | B．(0,1) | C．(1,2) | D．与k有关,无法确定 |