某数学兴趣小组在本校九年级学生中以“你最喜欢的一项体育运动”为主题进行了抽样调查,并将调查结果绘制成如图图表:
| 项目 |
篮球 |
乒乓球 |
羽毛球 |
跳绳 |
其他 |
| 人数 |
a |
12 |
10 |
5 |
8 |

请根据图表中的信息完成下列各题:
(1)本次共调查学生 名;
(2)a= ,表格中五个数据的中位数是 ;
(3)在扇形图中,“跳绳”对应的扇形圆心角是 °;
(4)如果该年级有450名学生,那么据此估计大约有 人最喜欢“乒乓球”.
如图,在平面直角坐标系中,有一条直线l: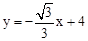 与x轴、y轴分别交于点M、N,一个高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移.
与x轴、y轴分别交于点M、N,一个高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移.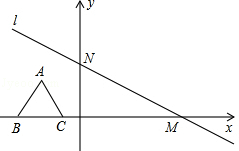
(1)在平移过程中,得到△A1B1C1,此时顶点A1恰落在直线l上,写出A1点的坐标 ;
(2)继续向右平移,得到△A2B2C2,此时它的外心P恰好落在直线l上,求P点的坐标;
(3)在直线l上是否存在这样的点,与(2)中的A2、B2、C2任意两点能同时构成三个等腰三角形?如果存在,求出点的坐标;如果不存在,说明理由.
在△ABC中,BC=a,AC=b,AB=c,设c为最长边,当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,探究△ABC的形状(按角分类).
(1)当△ABC三边分别为6、8、9时,△ABC为 三角形;当△ABC三边分别为6、8、11时,△ABC为 三角形.
(2)猜想,当a2+b2 c2时,△ABC为锐角三角形;当a2+b2 c2时,△ABC为钝角三角形.
(3)判断当a=2,b=4时,△ABC的形状,并求出对应的c的取值范围.
已知:直线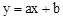 过抛物线
过抛物线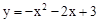 的顶点P,如图所示.
的顶点P,如图所示.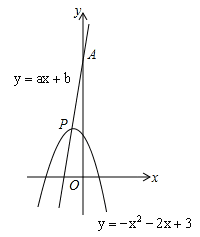
(1)顶点P的坐标是 ;
(2)若直线y=ax+b经过另一点A(0,11),求出该直线的表达式;
(3)在(2)的条件下,若有一条直线y=mx+n与直线y=ax+b关于x轴成轴对称,求直线y=mx+n与抛物线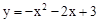 的交点坐标.
的交点坐标.
如图,二次函数的图象与x轴相交于点A(﹣3,0)、B(﹣1,0),与y轴相交于点C(0,3),点P是该图象上的动点;一次函数y=kx﹣4k(k≠0)的图象过点P交x轴于点Q.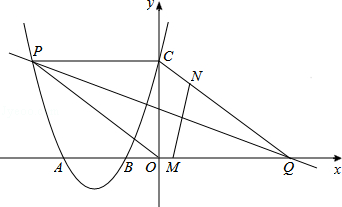
(1)求该二次函数的解析式;
(2)当点P的坐标为(﹣4,m)时,求证:∠OPC=∠AQC;
(3)点M,N分别在线段AQ、CQ上,点M以每秒3个单位长度的速度从点A向点Q运动,同时,点N以每秒1个单位长度的速度从点C向点Q运动,当点M,N中有一点到达Q点时,两点同时停止运动,设运动时间为t秒.连接AN,当△AMN的面积最大时,
①求t的值;
②直线PQ能否垂直平分线段MN?若能,请求出此时点P的坐标;若不能,请说明你的理由.
(1)如图(1)点P是正方形ABCD的边CD上一点(点P与点C,D不重合),点E在BC的延长线上,且CE=CP,连接BP,DE.求证:△BCP≌△DCE;
(2)直线EP交AD于F,连接BF,FC.点G是FC与BP的交点.
①若CD=2PC时,求证:BP⊥CF;
②若CD=n•PC(n是大于1的实数)时,记△BPF的面积为S1,△DPE的面积为S2.求证:S1=(n+1)S2.