(1)已知方程x2+px+q=0(p2-4q≥0)的两根为x1、x2,求证:x1+x2=-p,x1·x2=q.(2)已知抛物线y=x2+px+q与x轴交于点A、B,且过点(―1,―1),设线段AB的长为d,当p为何值时,d2取得最小值并求出该最小值.
解不等式组: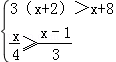 并把它的解集在数轴上表示出来.
并把它的解集在数轴上表示出来.
我市化工园区一化工厂,组织20辆汽车装运A、B、C三种化学物资共200吨到某地.按计划20辆汽车都要装运,每辆汽车只能装运同一种物资且必须装满.请结合表中提供的信息,解答下列问题:
(1)设装运A种物资的车辆数为x,装运B种物资的车辆数为y.求y与x的函数关系式;
(2)如果装运A种物资的车辆数不少于5辆,装运B种物资的车辆数不少于4辆,那么车辆的安排有几种方案?并写出每种安排方案;
(3)在(2)的条件下,若要求总运费最少,应采用哪种安排方案?请求出最少总运费.
| 物资种类 |
A |
B |
C |
| 每辆汽车运载量(吨) |
12 |
10 |
8 |
| 每吨所需运费(元/吨) |
240 |
320 |
200 |
小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1 m,小明爸爸与家之间的距离为s2m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.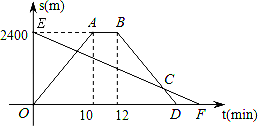
(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
点P(x,y)在第一象限,且x+y=10,点A的坐标为(8,0),设原点为O,△OPA的面积为S.
(1)求S与x的函数关系式,写出x的取值范围,画出这个函数图象;
(2)当S=12时,求点P的坐标;
(3)△OPA的面积能大于40吗?为什么?
已知一次函数的图象经过点(3,6)与点( ,﹣
,﹣ ),求这个函数的解析式.
),求这个函数的解析式.