如图,在平面直角坐标系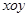 中,点
中,点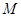 在
在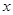 轴的正半轴上, ⊙
轴的正半轴上, ⊙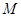 交
交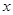 轴于
轴于 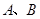 两点,交
两点,交 轴于
轴于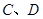 两点,且
两点,且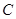 为
为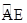 的中点,
的中点,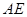 交
交 轴于
轴于 点,若点
点,若点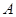 的坐标为(-2,0),
的坐标为(-2,0),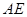
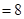
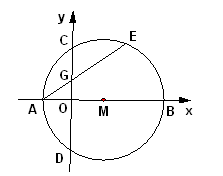
(1)求点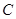 的坐标.
的坐标.
(2)连结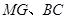 ,求证:
,求证: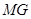 ∥
∥
(3) 如图10-2,过点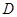 作⊙
作⊙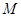 的切线,交
的切线,交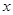 轴于点
轴于点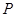 .动点
.动点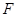 在⊙
在⊙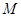 的圆周上运动时,
的圆周上运动时,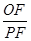 的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
一辆货车和一辆小轿车同时从甲地出发,货车匀速行驶至乙地,小轿车中途停车休整后提速行驶至乙地.货车的路程 (km),小轿车的路程
(km),小轿车的路程 (km)与时间x(h)的对应关系如图所示.
(km)与时间x(h)的对应关系如图所示.
(1)甲乙两地相距多远?小轿车中途停留了多长时间?
(2)①写出 与x的函数关系式;
与x的函数关系式;
②当x≥5时,求 与x的函数解析式;
与x的函数解析式;
(3)货车出发多长时间与小轿车首次相遇?相遇时与甲地的距离是多少?
如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
(1)求证:DC=DE;
(2)若tan∠CAB= ,AB=3,求BD的长.
,AB=3,求BD的长.
将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.
(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.
如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)
如图,▱ABCD中,点E,F在直线AC上(点E在F左侧),BE∥DF.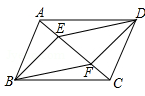
(1)求证:四边形BEDF是平行四边形;
(2)若AB⊥AC,AB=4,BC=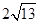 ,当四边形BEDF为矩形时,求线段AE的长.
,当四边形BEDF为矩形时,求线段AE的长.