如图1，已知OA和OB是⊙O的半径，并且OA⊥OB，P是OA上任一点(不与O、A重合)，BP的延长线交⊙O于Q，过Q点作⊙O的切线交OA的延长线于R.说明：RP=RQ.
运动探求.
(1)如图2，若OA向上平移，变化一中的结论还成立吗？(只需交待判断) 答：_________.
(2)如图3，如果P在OA的延长线上时，BP交⊙O于Q，过点Q作⊙O的切线交OA的延长线于R，原题中的结论还成立吗？为什么？
（1）先化简再求值：求
的值，其中
.
（2）已知A
，B
，且多项式
的值与字母
的取值无关，求
的值.
解方程：（每题3分）①
②
计算或化简：（每题3分）
①8＋(－10)―(―5)
②
③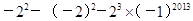
④(5x－3y)－(2x－y)
⑤a2－a－[2a－(3a2＋a)]
如图，直角坐标系中，点A的坐标为（1，0），以线段OA为边在第四象限内作等边△AOB，点C为
正半轴上一动点（OC＞1），连结BC，以线段BC为边在第四象限内作等边△CBD，直线DA交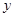
轴于点E．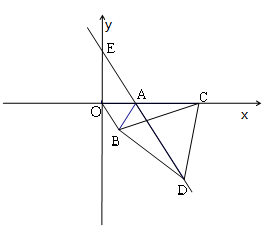
（1）△OBC与△ABD全等吗？判断并证明你的结论；
（2）将等边△AOB沿轴翻折，B点的对称点为B'
①点B'会落在直线DE上么？请说明理由．
②随着点C位置的变化，点E的位置是否会发生变化? 若没有变化，求直接写出点E
已知某种水果的批发单价与批发量的函数关系如图所示．
（1）请说明图中①、②两段函数图象的实际意义．
（2）写出批发该种水果的资金金额w（元）与批发量m（kg）之间的函数关系式；在下图的坐标系中画出该函数图象；指出金额在什么范围内，以同样的资金可以批发到较多数量的该种水果．